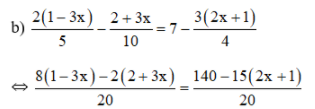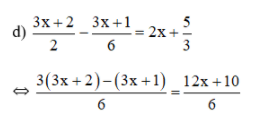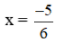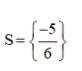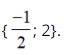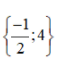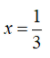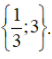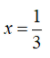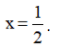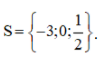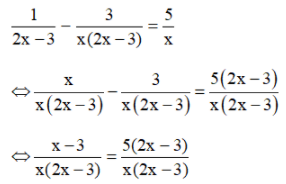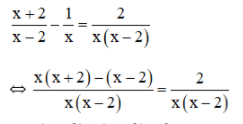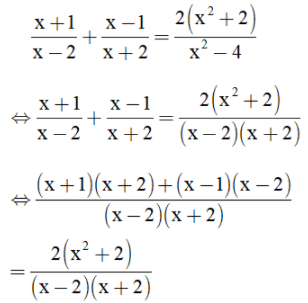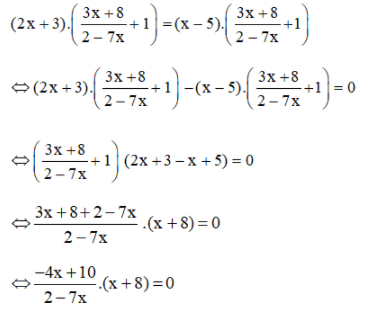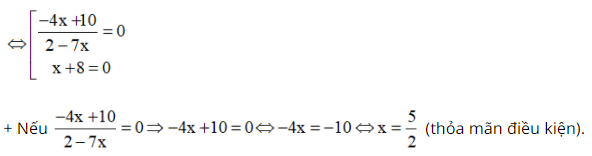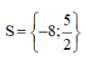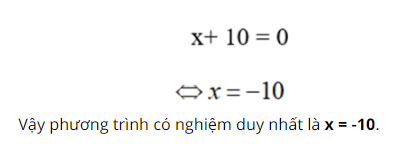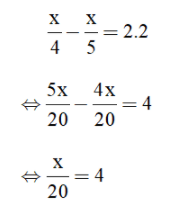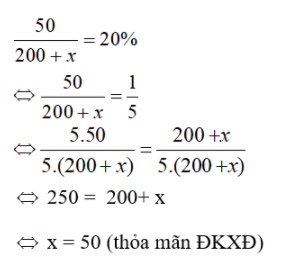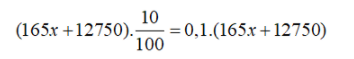Bài 50, 51, 52, 53, 54, 55, 56 trang 33, 34 SGK Toán 8 tập 2 - Ôn tập chương 3Bài 50, 51, 52 trang 33; bài 53, 54, 55, 56 trang 34 SGK Toán 8 tập 2 - Ôn tập chương 3. Bài 54 trang 34: Một canô xuôi dòng từ bến A đến bến B mất 4 giờ và ngược dòng từ bến B về bến A mất 5 giờ. Tính khoảng cách giữa hai bến A và B, biết rằng vận tốc của dòng nước là 2 km/h. Bài 50 trang 33 SGK Toán lớp 8 tập 2 Câu hỏi: Giải các phương trình: a. \(3 - 4x\left( {25 - 2x} \right) = 8{x^2} + x - 300\) ; b. \(\dfrac{{2\left( {1 - 3x} \right)}}{5} - \dfrac{{2 + 3x}}{{10}} = 7 - \dfrac{{3\left( {2x + 1} \right)}}{4}\) ; c. \(\dfrac{{5x + 2}}{6} - \dfrac{{8x - 1}}{3} = \dfrac{{4x + 2}}{5} - 5\) ; d. \(\dfrac{{3x + 2}}{2} - \dfrac{{3x + 1}}{6} = 2x + \dfrac{5}{3}\) . Lời giải: a) 3 – 4x(25 – 2x) = 8x2 + x – 300 ⇔ 3 – 4x.25 + 4x.2x = 8x2 + x – 300 ⇔ 3 – 100x + 8x2 = 8x2 + x – 300 ⇔ -100x – x = -300 – 3 ⇔ -101x = -303 ⇔ x = 3. Vậy phương trình có tập nghiệm S = {3}.
⇔ 8(1 – 3x) – 2(2 + 3x) = 140 – 15(2x + 1) ⇔ 8 – 24x – 4 – 6x = 140 – 30x – 15 ⇔ 4 – 30x = 125 – 30x ⇔ 0x = 121 (vô lý) Vậy phương trình vô nghiệm. 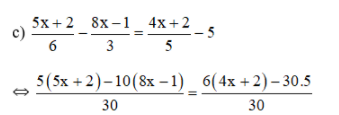 ⇔ 5(5x + 2) – 10(8x – 1) = 6(4x + 2) – 150 ⇔ 25x + 10 – 80x + 10 = 24x + 12 – 150 ⇔ 20 – 55x = 24x – 138 ⇔ -55x – 24x = -138 – 20 ⇔ -79x = -158 ⇔ x = 2. Vậy phương trình có tập nghiệm S = {2}.
⇔ 3(3x + 2) – (3x + 1) = 12x + 10 ⇔ 9x + 6 – 3x – 1 = 12x + 10 ⇔ 6x + 5 = 12x + 10 ⇔ 6x – 12x = 10 – 5 ⇔ -6x = 5 ⇔ Vậy phương trình có tập nghiệm Bài 51 trang 33 SGK Toán lớp 8 tập 2 Câu hỏi: Giải các phương trình sau bằng cách đưa về phương trình tích: a. \(\left( {2x + 1} \right)\left( {3x - 2} \right) = \left( {5x - 8} \right)\left( {2x + 1} \right)\) b. \(4{x^2} - 1 = \left( {2x + 1} \right)\left( {3x - 5} \right)\) c. \({\left( {x + 1} \right)^2} = 4\left( {{x^2} - 2x + 1} \right);\) d. \(2{x^3} + 5{x^2} - 3x = 0\) Phương pháp: Sử dụng phương pháp đặt nhân tử chung để đưa phương trình đã cho về dạng phương trình tích. Lời giải: a) (2x + 1)(3x – 2) = (5x – 8)(2x + 1) ⇔ (2x + 1)(3x – 2) – (5x – 8)(2x + 1) = 0 ⇔ (2x + 1).[(3x – 2) – (5x – 8)] = 0 ⇔ (2x + 1).(3x – 2 – 5x + 8) = 0 ⇔ (2x + 1)(6 – 2x) = 0 ⇔ 2x + 1 = 0 hoặc 6 – 2x = 0 Nếu 2x + 1 = 0 ⇔ 2x = –1 ⇔ x = Nếu 6 – 2x = 0 ⇔ 6 = 2x ⇔ x = 3. Vậy phương trình có tập nghiệm S = b) 4x2 – 1 = (2x + 1)(3x – 5) ⇔ 4x2 – 1 – (2x + 1)(3x – 5) = 0 ⇔ (2x – 1)(2x + 1) – (2x + 1)(3x – 5) = 0 ⇔ (2x + 1)[(2x – 1) – (3x – 5)] = 0 ⇔ (2x + 1)(2x – 1 – 3x + 5) = 0 ⇔ (2x + 1)(4 – x) = 0 ⇔ 2x + 1= 0 hoặc 4 – x = 0 Nếu 2x + 1 = 0 ⇔ 2x = –1 ⇔ x = Nếu 4 – x = 0 ⇔ x = 4. Vậy phương trình có tập nghiệm S= c) (x + 1)2 = 4(x2 – 2x + 1) Cách 1: (x + 1)2 = 4(x2 – 2x + 1) ⇔ (x + 1)2 – 4(x2 – 2x + 1) = 0 ⇔ (x + 1)2 – 22. (x – 1)2 = 0 ⇔ (x + 1)2 – [ 2(x – 1)]2 =0 ⇔ [(x + 1) + 2(x – 1)].[(x + 1) – 2( x – 1)]= 0 ⇔ (x + 1 + 2x - 2)(x + 1 – 2x + 2) =0 ⇔ (3x – 1)(3 – x) = 0 ⇔ 3x – 1 = 0 hoặc 3 – x = 0 Nếu 3x – 1 = 0 ⇔ 3x = 1 ⇔ Nếu 3 – x = 0 ⇔ x = 3 Vậy tập nghiệm của phương trình đã cho là:S = * Cách 2: (x + 1)2 = 4(x2 – 2x + 1) ⇔ (x + 1)2 – 4(x2 – 2x + 1) = 0 ⇔ x2 + 2x +1 – 4x2 + 8x – 4 = 0 ⇔ –3x2 + 10x – 3 = 0 ⇔ (–3x2 + 9x) + (x – 3) = 0 ⇔ –3x(x – 3) + ( x – 3) = 0 ⇔ (x – 3).(–3x + 1) = 0 ⇔ x – 3 = 0 hoặc – 3x + 1= 0 +) x – 3 = 0 ⇔ x = 3 +) –3x + 1 = 0 ⇔ – 3x = – 1 ⇔ Vậy tập nghiệm của phương trình đã cho là: S= d) 2x3 + 5x2 – 3x = 0 ⇔ x(2x2 + 5x – 3) = 0 ⇔ x.(2x2 + 6x – x – 3) = 0 ⇔ x. [2x(x + 3) – (x + 3)] = 0 ⇔ x.(2x – 1)(x + 3) = 0 ⇔ x = 0 hoặc 2x – 1 = 0 hoặc x + 3 = 0 +) 2x – 1 = 0 ⇔ 2x = 1 ⇔ +) x + 3 = 0 ⇔ x = –3. Vậy phương trình có tập nghiệm S= Bài 52 trang 33 SGK Toán lớp 8 tập 2 Câu hỏi: Giải các phương trình: a. \(\dfrac{1}{{2x - 3}} - \dfrac{3}{{x\left( {2x - 3} \right)}} = \dfrac{5}{x}\) ; b. \(\dfrac{{x + 2}}{{x - 2}} - \dfrac{1}{x} = \dfrac{2}{{x\left( {x - 2} \right)}}\) ; c. \(\dfrac{{x + 1}}{{x - 2}} + \dfrac{{x - 1}}{{x + 2}} = \dfrac{{2\left( {{x^2} + 2} \right)}}{{{x^2} - 4}};\) d. \(\left( {2x + 3} \right)\left( {\dfrac{{3x + 8}}{{2 - 7x}} + 1} \right) \) \( = \left( {x - 5} \right)\left( {\dfrac{{3x + 8}}{{2 - 7x}} + 1} \right)\) Phương pháp: Bước 1: Tìm điều kiện xác định của phương trình. Bước 2: Quy đồng mẫu hai vế của phương trình rồi khử mẫu. Bước 3: Giải phương trình vừa nhận được. Bước 4: Kết luận, trong các giá trị của ẩn tìm được ở bước 3, các giá trị thỏa mãn điều kiện xác định chính là các nghiệm của phương trình đã cho. Lời giải: a) Điều kiện xác định: x ≠ 0 và x ≠
Suy ra: x – 3 = 5(2x – 3) ⇔ x – 3 = 10x – 15 ⇔ x – 10x = –15 + 3 ⇔ –9x = –12 ⇔ x = Vậy phương trình có tập nghiệm S = b) Điều kiện xác định: x ≠ 0; x ≠ 2.
⇒ x(x + 2) – (x – 2) = 2 ⇔ x2 + 2x – x + 2 = 2 ⇔ x2 + x = 0 ⇔ x(x + 1) = 0 ⇔ x = 0 hoặc x + 1 = 0. + x = 0 không thỏa mãn điều kiện xác định. + x + 1 = 0 ⇔ x = -1 (thỏa mãn điều kiện xác định). Vậy phương trình có tập nghiệm S = {-1}. c) Điều kiện xác định: x ≠ ±2.
⇒ (x + 1)(x + 2) + (x – 1)(x – 2) = 2(x2 + 2) ⇔ x2 + x + 2x + 2 + x2 – x – 2x + 2 = 2x2 + 4 ⇔ 2x2 + 4 = 2x2 + 4 ⇔ 0x = 0. Vậy phương trình nghiệm đúng với mọi x ≠ ±2. d) Điều kiện xác định: x ≠
+ Nếu x + 8 = 0 thì x = –8 (thỏa mãn điều kiện). Vậy phương trình có tập nghiệm là Bài 53 trang 34 SGK Toán lớp 8 tập 2 Câu hỏi: Giải phương trình: \(\dfrac{{x + 1}}{9} + \dfrac{{x + 2}}{8} = \dfrac{{x + 3}}{7} + \dfrac{{x + 4}}{6}\) Phương pháp: Cộng \(2\) vào hai vế của phương trình sau đó giải phương trình mới để tìm \( x\). Lời giải:
Bài 54 trang 33 SGK Toán lớp 8 tập 2 Câu hỏi: Một canô xuôi dòng từ bến A đến bến B mất 4 giờ và ngược dòng từ bến B về bến A mất 5 giờ. Tính khoảng cách giữa hai bến A và B, biết rằng vận tốc của dòng nước là 2 km/h. Phương pháp: Áp dụng công thức của bài toán chuyển động trên dòng nước: Nếu gọi vận tốc canô là v (km/h), vận tốc dòng nước là a (km/h), ta có: Khi xuôi dòng, vận tốc canô là: v + a Khi ngược dòng, vận tốc canô là: v - a Hiệu vận tốc \(= v + a - (v - a) = 2.a\). Vậy hiệu vận tốc =2. vận tốc dòng nước. Bước 1: Gọi khoảng cách giữa A và B là ẩn, đặt điều kiện cho ẩn. Bước 2: Biểu diễn các đại lượng khác qua ẩn Bước 3: Lập phương trình thông qua các mối liên hệ giữa các đại lượng, giải phương trình Bước 4: Kết luận Lời giải: Gọi x (km) là khoảng cách giữa hai bến A và B, với x > 0.
Vì vận tốc xuôi dòng lớn hơn vận tốc ngược dòng chính bằng 2 lần vận tốc dòng nước nên ta có phương trình:
x = 80 (thỏa mãn điều kiện). Vậy khoảng cách giữa hai bến A và B là 80km. (Giải thích tại sao hiệu vận tốc xuôi dòng và ngược dòng bằng 2 lần vận tốc dòng nước: Nếu gọi vận tốc canô là v (km/h), vận tốc dòng nước là a (km/h), ta có: Khi xuôi dòng: vận tốc canô = v + a Khi ngược dòng: vận tốc canô = v - a Hiệu vận tốc = v + a - (v - a) = 2a = 2 vận tốc dòng nước.) Bài 55 trang 34 SGK Toán lớp 8 tập 2 Câu hỏi: Biết rằng 200g một dung dịch chứa 50g muối. Hỏi phải pha thêm bao nhiêu gam nước vào dung dịch đó để được một dung dịch chứa 20% muối? Lời giải: Gọi x (g) là khối lượng nước phải pha thêm, với x > 0. Khối lượng dung dịch mới: 200 + x (g) Ta có: nồng độ dung dịch = số g muối / số g dung dịch. Vì khối lượng muối không đổi nên nồng độ dung dịch sau khi pha thêm nước bằng Theo đề bài, nồng độ dung dịch mới chứa 20% muối nên ta có phương trình:
Vậy phải pha thêm 50g nước để được dung dịch chứa 20% muối. Bài 56 trang 34 SGK Toán lớp 8 tập 2 Câu hỏi: Để khuyến khích tiết kiệm điện, giá điện sinh hoạt được tính theo kiểu lũy tiến, nghĩa là nếu người sử dụng càng nhiều điện thì giá mỗi số điện (1kw/h) càng tăng lên theo các mức như sau: Mức thứ nhất: Tính cho 100 số điện đầu tiên; Mức thứ hai: Tính cho số điện thứ 101 đến 150, mỗi số đắt hơn 150 đồng so với mức thứ nhất; Mức thứ ba: Tính cho số điện thứ 151 đến 200, mỗi số đắt hơn 200 đồng so với mức thứ hai; v.v... Ngoài ra người sử dụng còn phải trả thêm 10% thuế giá trị gia tăng (thuế VAT). Tháng vừa qua, nhà Cường dùng hết 165 số điện và phải trả 95700 đồng. Hỏi mỗi số điện ở mức thứ nhất giá là bao nhiêu? Phương pháp: - Gọi \(x\) (đồng) là giá điện ở mức thứ nhất \(x>0\). - Số tiền phải trả ở mức 1: \(100x\) (đồng). - Số tiền phải trả ở mức 2: \(50(x + 150)\) (đồng). - Số tiền phải trả ở mức 3: \(15(x + 150 +200)=15(x + 350)\) (đồng). - Số tiền phải trả chưa tính thuế VAT là: \(100x + 50(x + 150) + 15(x + 350)\) - Số tiền thuế VAT = 10% của \(100x + 50(x + 150) + 15(x + 350)\) - Số tiền phải trả = Số tiền phải trả chưa tính thuế VAT + Số tiền thuế VAT Giải phương trình biểu diễn số tiền phải trả ta tìm được số tiền của mỗi số điện ở mức thứ nhất. Lời giải: Gọi x (đồng) là giá mỗi số điện ở mức thứ nhất (x > 0). ⇒ Giá mỗi số điện ở mức 2 là: x + 150 (đồng) ⇒ Giá mỗi số điện ở mức 3 là: x + 150 + 200 = x + 350 (đồng) Nhà Cường dùng hết 165 số điện = 100 + 50 + 15. Như vậy nhà Cường phải đóng cho 100 số điện ở mức 1, 50 số điện ở mức 2 và 15 số điện ở mức 3. Giá tiền 100 số điện mức đầu tiên là: 100.x (đồng) Giá tiền 50 số điện mức thứ hai là: 50.(x + 150) (đồng) Giá tiền 15 số điện còn lại mức thứ ba là: 15.(x + 350) (đồng) ⇒ Số tiền điện (chưa tính VAT) của nhà Cường bằng: 100.x + 50.(x + 150) + 15.(x + 350) = 100x + 50x + 50.150 +15x +15.350 = 165x + 12750. Thuế VAT nhà Cường phải trả là: (165x + 12750).10%
Tổng số tiền điện nhà Cường phải đóng (tiền gốc + thuế) bằng: 165x + 12750 + 0,1.(165x + 12750) = 1,1.(165x + 12750). Thực tế nhà Cường hết 95700 đồng nên ta có phương trình: 1,1(165x + 12750) = 95700 ⇔ 165x + 12750 = 87000 ⇔ 165x = 74250 ⇔ x = 450 (đồng) (thỏa mãn điều kiện). Vậy mỗi số điện ở mức giá đầu tiên là 450 đồng. sachbaitap.com
Xem thêm tại đây:
Chương III. Phương trình bậc nhất một ẩn
|
-

Bài 1, 2, 3, 4 trang 37 SGK Toán 8 tập 2 - Liên hệ giữa thứ tự và phép cộng
Bài 1, 2, 3, 4 trang 37 SGK Toán 8 tập 2 - Liên hệ giữa thứ tự và phép cộng. Bài 4 trang 37 Đố: Một biển báo giao thông với nền trắng, số 20 màu đen, viền đỏ (xem minh họa ở hình bên) cho biết vận tốc tối đa mà các phương tiện giao thông được đi trên quãng đường có biển quy định là 20km/h. Nếu một ô tô đi trên đường đó có vận tốc là a (km/h) thì a phải thỏa mãn điều kiện nào trong các điều kiện sau?
-

Bài 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 trang 39, 40 SGK Toán 8 tập 2 - Liên hệ giữa thứ tự và phép nhân
Bài 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 trang 39, 40 SGK Toán 8 tập 2 - Liên hệ giữa thứ tự và phép nhân. Bài 5 trang 39 Mỗi khẳng định sau đúng hay sai? Vì sao?a) (-6).5 < (-5).5 ;b) (-6).(-3) < (-5).(-3);c) (-2003).(-2005) ≤ (-2005).2004;d) -3x2 ≤ 0.
-

Bài 15, 16, 17, 18 trang 43 SGK Toán 8 tập 2 -Bất phương trình một ẩn
Bài 15, 16, 17, 18 trang 43 SGK Toán 8 tập 2 - Bất phương trình một ẩn. Bài 16 trang 43 Viết và biểu diễn tập nghiệm trên trục số của mỗi bất phương trình sau: a) x < 4 ; b) x ≤ -2 c) x > -3 ; d) x ≥ 1
-

Bài 19, 20, 21, 22, 23, 24, 25, 26, 27 trang 47, 48 SGK Toán 8 tập 2 - Bất phương trình bậc nhất một ẩn
Bài 19, 20, 21, 22, 23, 24, 25, 26 trang 47;bài 27 trang 48 SGK Toán 8 tập 2 - Bất phương trình bậc nhất một ẩn. Bài 23 trang 47 Giải các bất phương trình và biểu diễn tập nghiệm trên trục số:a) 2x - 3 > 0 ; b) 3x + 4 < 0c) 4 - 3x ≤ 0 ; d) 5 - 2x ≥ 0.

 Tải ngay
Tải ngay