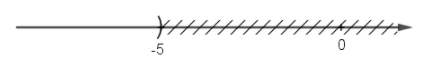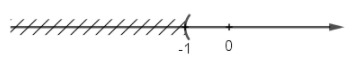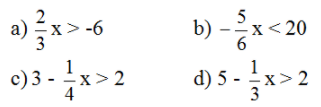Bài 19, 20, 21, 22, 23, 24, 25, 26, 27 trang 47, 48 SGK Toán 8 tập 2 - Bất phương trình bậc nhất một ẩnBài 19, 20, 21, 22, 23, 24, 25, 26 trang 47;bài 27 trang 48 SGK Toán 8 tập 2 - Bất phương trình bậc nhất một ẩn. Bài 23 trang 47 Giải các bất phương trình và biểu diễn tập nghiệm trên trục số:a) 2x - 3 > 0 ; b) 3x + 4 < 0c) 4 - 3x ≤ 0 ; d) 5 - 2x ≥ 0. Bài 19 trang 47 SGK Toán lớp 8 tập 2 Câu hỏi: Giải các bất phương trình (theo quy tắc chuyển vế): a) x - 5 > 3 b) x - 2x < -2x + 4 c) -3x > -4x + 2 d) 8x + 2 < 7x - 1 Phương pháp: Áp dụng qui tắc chuyển vế: Khi chuyển một hạng tử của bất phương trình từ vế này sang vế kia ta đổi dấu hạng tử đó. Lời giải: (Áp dụng quy tắc: chuyển vế - đổi dấu) a) x - 5 > 3 ⇔ x > 3 + 5 (chuyển -5 từ vế trái sang vế phải và đổi dấu thành 5) ⇔ x > 8. Vậy nghiệm của bất phương trình là x > 8. b) x - 2x < -2x + 4 ⇔ x - 2x + 2x < 4 ⇔ x < 4 Vậy nghiệm của bất phương trình là x < 4. c) -3x > -4x + 2 ⇔ -3x + 4x > 2 ⇔ x > 2 Vậy nghiệm của bất phương trình là x > 2. d) 8x + 2 < 7x - 1 ⇔ 8x - 7x < -1 - 2 ⇔ x < -3 Vậy nghiệm của bất phương trình là x < -3. Bài 20 trang 47 SGK Toán lớp 8 tập 2 Câu hỏi: Giải các bất phương trình (theo quy tắc nhân): a) 0,3x > 0,6 ; b) -4x < 12 c) -x > 4 ; d) 1,5x > -9 Phương pháp: Áp dụng qui tắc nhân với một số: Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải: - Giữ nguyên chiều bất phương trình nếu số đó dương. - Đổi chiều bất phương trình nếu số đó âm. Lời giải:
Bài 21 trang 47 SGK Toán lớp 8 tập 2 Câu hỏi: Giải thích sự tương đương sau: a) x - 3 > 1 ⇔ x + 3 > 7 b) -x < 2 ⇔ 3x > -6 Phương pháp: Áp dụng định nghĩa hai bất phương trình tương đương: Hai bất phương trình tương đương là hai bất phương trình có cùng tập nghiệm. Lời giải: a) x – 3 > 1 ⇔ x – 3 + 6 > 1 + 6 (Cộng 6 vào cả hai vế). Hay x + 3 > 7.. Vậy hai bpt trên tương đương. b) –x < 2 ⇔ (-x).(-3) > 2.(-3) (Nhân cả hai vế với -3 < 0, BPT đổi dấu) ⇔ 3x > -6. Vậy hai BPT trên tương đương. Bài 22 trang 47 SGK Toán lớp 8 tập 2 Câu hỏi: Giải các bất phương trình và biểu diễn tập nghiệm trên trục số: a) 1,2x < -6 ; b) 3x + 4 > 2x + 3 Phương pháp: Áp dụng quy tắc nhân Khi ta nhân (hoặc chia) hai vế bất phương trình với 1 số âm thì ta được bất phương trình mới ngược chiều với bất phương trình ban đầu. Lời giải: a) 1,2x < -6 ⇔1,2 x : 1,2 < -6 : 1,2 ⇔ x < - 5 Vậy nghiệm của bất phương trình là x < -5.
b) 3x + 4 > 2x + 3 ⇔ 3x - 2x > 3 - 4 (chuyển vế 2x và 4, đổi dấu hạng tử). ⇔ x > -1 Vậy nghiệm của bất phương trình là x > -1.
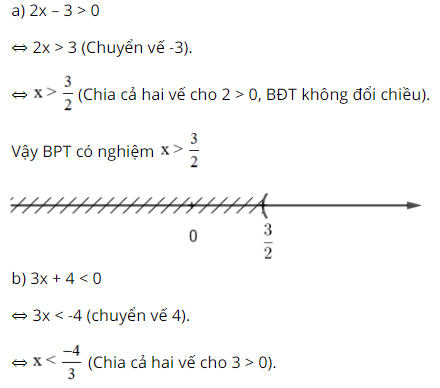
Bài 23 trang 47 SGK Toán lớp 8 tập 2 Câu hỏi: Giải các bất phương trình và biểu diễn tập nghiệm trên trục số: a) 2x - 3 > 0 ; b) 3x + 4 < 0 c) 4 - 3x ≤ 0 ; d) 5 - 2x ≥ 0 Phương pháp: Áp dụng - Qui tắc chuyển vế Khi chuyển một hạng tử của bất phương trình từ vế này sang vế kia ta đổi dấu hạng tử đó. - Quy tắc nhân với một số Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải: + Giữ nguyên chiều bất phương trình nếu số đó dương. + Đổi chiều bất phương trình nếu số đó âm. Lời giải:
Bài 24 trang 47 SGK Toán lớp 8 tập 2 Câu hỏi: Giải các bất phương trình: a) 2x - 1 > 5 ; b) 3x - 2 < 4 c) 2 - 5x ≤ 17 ; d) 3 - 4x ≥ 19 Phương pháp: Áp dụng: Quy tắc chuyển vế và quy tắc nhân hai vế với một số. Lời giải: a) 2x - 1 > 5 ⇔ 2x > 1 + 5 (Chuyển vế và đổi dấu hạng tử -1) ⇔ 2x > 6 ⇔ x > 3 (Chia cả hai vế cho 2 > 0, BPT không đổi chiều). Vậy nghiệm của bất phương trình là x > 3. b) 3x - 2 < 4 ⇔ 3x < 4 + 2 (Chuyển vế và đổi dấu hạng tử -2) ⇔ 3x < 6 ⇔ x < 2 (Chia cả hai vế cho 3 > 0, BPT không đổi chiều). Vậy nghiệm của bất phương trình là x < 2. c) 2 - 5x ≤ 17 ⇔ -5x ≤ 17 - 2 (Chuyển vế và đổi dấu hạng tử 2) ⇔ -5x ≤ 15 ⇔ x ≥ -3 (Chia cả hai vế cho -5 < 0, BPT đổi chiều). Vậy nghiệm của bất phương trình là x ≥ - 3 d) 3 - 4x ≥ 19 ⇔ -4x ≥ 19 - 3 (Chuyển vế và đổi dấu hạng tử 3) ⇔ -4x ≥ 16 ⇔ x ≤ -4 (Chia cả hai vế cho -4 < 0, BPT đổi chiều). Vậy nghiệm của bất phương trình là x ≤ -4 Bài 25 trang 47 SGK Toán lớp 8 tập 2 Câu hỏi: Giải các bất phương trình:
Phương pháp: Áp dụng: Quy tắc chuyển vế và quy tắc nhân hai vế với một số. Lời giải:
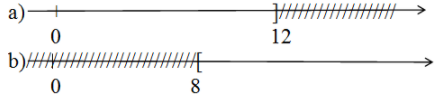
Bài 26 trang 47 SGK Toán lớp 8 tập 2 Câu hỏi: Hình vẽ sau biểu diễn tập nghiệm của bất phương trình nào? (Kể ba bất phương trình có cùng tập nghiệm).
Phương pháp: Áp dụng qui tắc biểu diễn tập nghiệm trên trục số. Lời giải: a) Hình a) biểu diễn tập nghiệm của bất phương trình: x ≤ 12 hoặc x + 4 ≤ 16 hoặc 2x + 1 ≤ 25 b) Hình biểu diễn tập nghiệm của bất phương trình: x ≥ 8 hoặc x + 3 ≥ 11 hoặc 3 – 2x ≤ -13. Bài 27 trang 48 SGK Toán lớp 8 tập 2 Câu hỏi: Đố: Kiểm tra xem giá trị x = -2 có là nghiệm của bất phương trình sau không? a) x + 2x2 – 3x3 + 4x4 – 5 < 2x2 – 3x3 + 4x4 – 6; b) (-0,001)x > 0,003. Phương pháp: Bước 1: Giải tìm tập nghiệm của bất phương trình Bước 2: Thay giá trị \(x=-2\) vào tập nghiệm của bất phương trình: +) Nếu cho khẳng định đúng thì \(x=-2\) là nghiệm của bất phương trình +) Nếu cho khẳng định sai thì \(x=-2\) không là nghiệm của bất phương trình. Lời giải: a) x + 2x2 - 3x3 + 4x4 - 5 < 2x2 - 3x3 + 4x4 - 6 ⇔ x < 2x2 - 3x3 + 4x4 - 6 - 2x2 + 3x3 - 4x4 + 5 (chuyển vế - đổi dấu) ⇔ x < -1 (*) Vì -2 < -1 nên -2 là nghiệm của bất phương trình Vậy x = -2 là nghiệm của bất phương trình. b) (-0,001)x > 0,003 ⇔ x < -3 (chia cả hai vế cho -0,001) Vì -2 > -3 nên -2 không phải nghiệm của bất phương trình Vậy x = -2 không là nghiệm của bất phương trình. sachbaitap.com
Xem thêm tại đây:
Chương IV. Bất phương trình bậc nhất một ẩn
|
-

Bài 28, 29, 30, 31, 32, 33, 34 trang 48, 49 SGK Toán 8 tập 2 - Luyện tập
Bài 28, 29, 30, 31, 32, 33 trang 48; bài 34 trang 49 SGK Toán 8 tập 2 - Luyện tập. Bài 30. Một người có số tiền không quá 70000 đồng gồm 15 tờ giấy bạc với hai loại mệnh giá: loại 2000 đồng và loại 5000 đồng. Hỏi người đó có bao nhiêu tờ giấy bạc loại 5000 đồng?
-

Bài 35, 36, 37 trang 51 SGK Toán 8 tập 2 - Phương trình chứa dấu giá trị tuyệt đối
Bài 35, 36, 37 trang 51 SGK Toán 8 tập 2 - Phương trình chứa dấu giá trị tuyệt đối. Bài 35 trang 51 Bỏ dấu giá trị tuyệt đối và rút gọn các biểu thức:
-

Bài 38, 39, 40, 41, 42, 43, 45 trang 53, 54 SGK Toán 8 tập 2 - Ôn tập chương 4
Bài 38, 39, 40, 41, 42, 43 trang 53; bài 44, 45 trang 54 SGK Toán 8 tập 2 - Ôn tập chương 4. Bài 38 trang 53:Cho (m > n), chứng minh: a) (m + 2 > n +2); b) (-2m < -2n); c) (2m -5 > 2n -5); d) (4 – 3m < 4 – 3n).
-

Bài 1, 2, 3, 4, 5 trang 58, 59 SGK Toán 8 tập 2 - Định lí Ta-lét trong tam giác
Bài 1 trang 58; bài 2, 3, 4, 5 trang 59 SGK Toán 8 tập 2 - Định lí Ta-lét trong tam giác. Bài 3 Cho biết độ dài của AB gấp 5 lần độ dài của CD và độ dài của A'B' gấp 12 lần độ dài của CD. Tính tỉ số của hai đoạn thẳng AB và A'B'.

 Tải ngay
Tải ngay