Bài 5.20 trang 222 sách bài tập (SBT) - Giải tích 12Tính: Tính: a) \(\int\limits_{ - 1}^2 {(5{x^2} - x + {e^{0,5x}})dx} \) b) \(\int\limits_{0,5}^2 {(2\sqrt x - {3 \over {{x^3}}} + \cos x)dx} \) c) \(\int\limits_1^2 {{{dx} \over {\sqrt {2x + 3} }}} \) (đặt \(t = \sqrt {2x + 3} \) ) d) \(\int\limits_1^2 {\root 3 \of {3{x^3} + 4} {x^2}dx} \) (đặt \(t = \root 3 \of {3{x^3} + 4} \)) e) \(\int\limits_{ - 2}^2 {(x - 2)|x|dx} \) g) \(\int\limits_1^0 {x\cos xdx} \) h)\(\int\limits_{{\pi \over 6}}^{{\pi \over 2}} {{{1 + \sin 2x + \cos 2x} \over {\sin x + \cos x}}} dx\) i) \(\int\limits_0^{{\pi \over 2}} {{e^x}\sin xdx} \) k) \(\int\limits_1^e {{x^2}{{\ln }^2}xdx} \) Hướng dẫn làm bài a) Đáp số: \(13{1 \over 2} + 2(e - {1 \over {\sqrt e }})\) b) Đáp số: \({{7\sqrt 2 } \over 3} - 5{5 \over 8} + \sin 2 - \sin {1 \over 2}\) c) Đáp số: \(\sqrt 7 - \sqrt 5 \) d) Đổi biến \(t = \root 3 \of {3{x^3} + 4} \) \(\Rightarrow {t^3} = 3{x^3} + 4 \Rightarrow 3{t^2}dt = 9{x^2}dx \Rightarrow {x^2}dx = {1 \over 3}{t^2}dt\) Ta có \(\eqalign{ e) \(\eqalign{ g) \(\eqalign{& \int\limits_1^0 {x\cos xdx = x\sin x\left| {\matrix{0 \cr 1 \cr} } \right.} - \int\limits_1^0 {\sin xdx} \cr & = - \sin 1 + \cos x\left| {\matrix{0 \cr 1 \cr} } \right. = 1 - (\sin 1 + \cos 1) \cr} \) h) Ta có: \(\eqalign{ Từ đó, ta có đáp số là 1. i) Áp dụng phương pháp tính tích phân từng phần hai lần, cả hai lần đều đặt \({e^x}dx = dv \Rightarrow v = {e^x}\) . Ta có: \(\eqalign{& I = \int\limits_0^{{\pi \over 2}} {{e^x}\sin xdx} = {e^x}\sin x\left| {\matrix{{{\pi \over 2}} \cr 0 \cr} } \right. - \int\limits_0^{{\pi \over 2}} {{e^x}\cos xdx} \cr & = {e^{{\pi \over 2}}} - \left[ {{e^x}\cos x\left| {\matrix{{{\pi \over 2}} \cr 0 \cr} + \int\limits_0^{{\pi \over 2}} {{e^x}\sin xdx} } \right.} \right] \cr & = {e^{{\pi \over 2}}} + 1 - I \cr & \Rightarrow I = {{{e^{{\pi \over 2}}} + 1} \over 2} \cr} \) k) Lấy tích phân theo phương pháp tính tích phân từng phầ;n hai lần: lần thứ nhất đặt \(u = {\ln ^2}x\) , lần thứ hai đặt \(u = \ln x\) và có đáp số là \({1 \over {27}}(5{e^3} - 2)\). Sachbaitap.com
Xem lời giải SGK - Toán 12 - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
BÀI TẬP ÔN TẬP CUỐI NĂM - GIẢI TÍCH 12
|
-
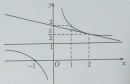
Bài 5.21 trang 223 sách bài tập (SBT) - Giải tích 12
Tính diện tích của hình phẳng giới hạn bởi các đường sau:
-
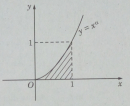
Bài 5.22 trang 223 sách bài tập (SBT) - Giải tích 12
Tính thể tích của vật thể tròn xoay khi quay các hình phẳng giới hạn bởi các đường sau quanh trục Ox:
-
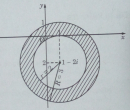
Bài 5.24 trang 223 sách bài tập (SBT) - Giải tích 12
Tìm tập hợp các điểm biểu diễn số phức z trên mặt phẳng tọa độ thỏa mãn các điều kiện:

 Tải ngay
Tải ngay