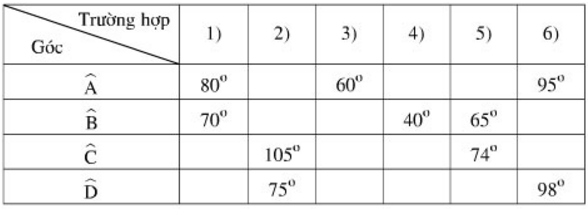
Bài 53, 54, 55 trang 89 SGK Toán 9 tập 2 - Tứ giác nội tiếpGiải bài 53, 54, 55 trang 89 sách giáo khoa (SGK) Toán lớp 9 tập 2 bài Tứ giác nội tiếp. Bài 54 Tứ giác ABCD có góc ABC + góc ADC = 180o. Chứng minh rằng các đường trung trực của AC, BD, AB cùng đi qua một điểm Bài 53 trang 89 SGK Toán lớp 9 tập 2 Câu hỏi: Biết ABCD là tứ giác nội tiếp. Hãy điền vào ô trống trong bảng sau (nếu có thể ):
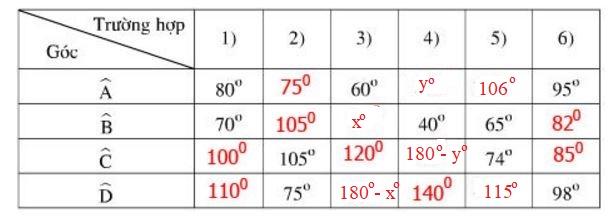
Lời giải: Theo đề bài ta có \(ABCD\) là tứ giác nội tiếp \( \Rightarrow \left\{ \begin{array}{l}\widehat A + \widehat C = {180^0}\\\widehat B + \widehat D = {180^0}\end{array} \right..\) - Trường hợp 1: Ta có: \(\widehat A + \widehat C = {180^0}\) \(\Rightarrow \widehat C = {180^0}-\widehat A= {180^0} - {80^0} = {100^0}.\) \(\widehat B + \widehat D = {180^0} \) \(\Rightarrow \widehat D = {180^0} - \widehat B = {180^0} - {70^0} = {110^0}.\) Vậy các góc còn lại là: \(\widehat{C}= 100^0,\) \(\widehat{D} = 110^0.\) - Trường hợp 2: \(\begin{array}{l} Ta \, \, có: \, \, - Trường hợp 3: Ta có: \(\widehat A + \widehat C = {180^0} \) \(\Rightarrow \widehat C = {180^0}-\widehat A= {180^0} - {60^0} = {120^0}.\) Có \( \widehat B + \widehat D = {180^0}.\) Gọi \(\widehat{B} = x^0\) thì \(\widehat{D}=180^0-x^0\) - Trường hợp 4: \(\widehat{D}=180^0-\widehat{B}=180^0 – 40^0= 140^0.\) Còn lại \(\widehat{A}+ \widehat{C}= 180^0.\) Gọi \(\widehat{A} = y^0\) thì \(\widehat{C}=180^0-y^0\) - Trường hợp 5: \(\widehat{A}=180^0-\widehat{C}=180^0–74^0=106^0.\) \(\widehat{B}= 180^0-\widehat{D}=180^0–65^0=115^0.\) - Trường hợp 6: \(\widehat{C}=180^0-\widehat{A}=180^0–95^0=85^0.\) \(\widehat{B}=180^0-\widehat{D}=180^0– 98^0=82^0.\) Vậy điền vào ô trống ta được bảng sau:
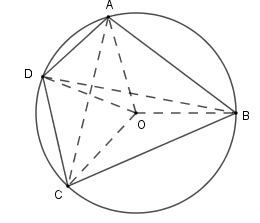
Bài 54 trang 89 SGK Toán lớp 9 tập 2 Câu hỏi: Tứ giác ABCD có góc ABC + góc ADC = 180o. Chứng minh rằng các đường trung trực của AC, BD, AB cùng đi qua một điểm. Lời giải:
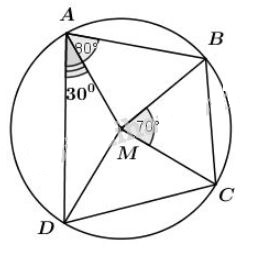
Tứ giác \(ABCD\) có \(\widehat{ABC}+ \widehat{ADC}= 180^0\) mà hai góc \(\widehat{ABC}\) và \( \widehat{ADC}\) là hai góc ở vị trí đối nhau nên tứ giác \(ABCD\) là tứ giác nội tiếp. Gọi \(O\) là tâm đường tròn ngoại tiếp tứ giác \(ABCD\), khi đó \(OA=OB=OC=OD\) (cùng bằng bán kính của đường tròn \( (O) \) ) + Vì \(OA = OB\) nên \(O\) thuộc đường trung trực của đoạn \(AB\) (định lí) + Vì \(OA = OC\) nên \(O\) thuộc đường trung trực của đoạn \(AC\) (định lí) + Vì \(OD = OB\) nên \(O\) thuộc đường trung trực của đoạn \(BD\) (định lí) Do đó các đường trung trực của \(AB, \, BD, \, AC\) cùng đi qua tâm \(O\) của đường tròn ngoại tiếp tứ giác \(ABCD\). Bài 55 trang 89 SGK Toán lớp 9 tập 2 Câu hỏi: Cho \(ABCD\) là một tứ giác nội tiếp đường tròn tâm \(M,\) biết \(\widehat {DAB}= 80^0\), \(\widehat {DAM}= 30^0,\) \(\widehat {BMC}= 70^0\). Hãy tính số đo các góc \(\widehat {MAB},\) \(\widehat {BCM},\) \(\widehat {AMB},\) \(\widehat {DMC},\) \(\widehat {AMD},\) \(\widehat {MCD}\) và \(\widehat {BCD}.\) Lời giải:
Vì AM nằm giữa AD và AB nên \(\widehat {MAB}+\widehat {DAM}= \widehat {DAB}\). Do đó, \(\widehat {MAB} = \widehat {DAB} - \widehat {DAM} = {80^0} - {30^0} = {50^0}\) (1) +) \(∆MBC\) là tam giác cân cân tại \(M\) \((MB= MC)\) nên \(\displaystyle \widehat {BCM} = {{{{180}^0} - {{70}^0}} \over 2} = {55^0}\) (2) +) \(∆MAB\) là tam giác cân tại \(M\) \((do MA=MB)\) nên \(\widehat {MAB} =\widehat {ABM} = {50^0}\) (theo (1)) Vậy \(\widehat {AMB} = {180^0} - {2.50^0} = {80^0}.\) Ta có: \(\widehat {BAD}=\dfrac{sđ\overparen{BCD}}{2}\) (số đo góc nội tiếp bằng nửa số đo của cung bị chắn). \(\Rightarrow sđ\overparen{BCD}=2.\widehat {BAD} = {2.80^0} = {160^0}.\) Mà \(sđ\overparen{BC}= \widehat {BMC} = {70^0}\) (số đo góc ở tâm bằng số đo cung bị chắn). Vậy \(sđ\overparen{DC}={160^0} - {70^0} = {90^0}\) (vì C nằm trên cung nhỏ cung \(BD\)). \(\Rightarrow\) \(\widehat {DMC} = {90^0}.\) (4) Ta có: \(∆MAD\) là tam giác cân cân tại \(M \) \((MA= MD).\) \(\Rightarrow\) \(\widehat {AMD} = {180^0} - {2.30^0}=120^0\) (5) Có \(∆MCD\) là tam giác vuông cân tại \(M\) \((MC= MD)\) và \(\widehat {DMC} = {90^0}\) \(\Rightarrow\) \(\widehat {MCD} = \widehat {MDC} = {45^0}.\) (6) Theo (2) và (6) và vì CM là tia nằm giữa hai tia \(CB, \, CD\) ta có: \(\widehat {BCD} =\widehat{BCM}+\widehat{MCD} = 55^0+45^0 = {100^0}.\) Sachbaitap.com
Xem thêm tại đây:
Bài 7. Tứ giác nội tiếp
|
-

Bài 56, 57, 58, 59, 60 trang 89, 90 SGK Toán 9 tập 2 - Luyện tập
Giải bài 56, 57 trang 89; bài 58, 59, 60 trang 90 sách giáo khoa (SGK) Toán lớp 9 tập 2 bài Luyện tập - Tứ giác nội tiếp. Bài 59 Cho hình bình hành ABCD. Đường tròn đi qua ba đỉnh A, B, C cắt đường thẳng CD tại P khác C. Chứng minh AP = AD.
-

Bài 61, 62, 63, 64 trang 91, 92 SGK Toán 9 tập 2 - Đường tròn ngoại tiếp. Đường tròn nội tiếp
Giải bài 61, 62 trang 91; bài 63, 64 trang 92 sách giáo khoa (SGK) Toán lớp 9 tập 2 bài Đường tròn ngoại tiếp. Đường tròn nội tiếp. Bài 63 Vẽ hình lục giác đều, hình vuông, tam giác đều cùng nội tiếp đường tròn (O; R) rồi tính cạnh của các hình đó theo R.

 Tải ngay
Tải ngay