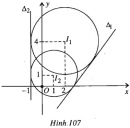
Bài 53 trang 108 SBT Hình học 10 Nâng caoGiải bài tập Bài 53 trang 108 SBT Hình học 10 Nâng cao Cho đường tròn \((C): {x^2} + {y^2} - 2x + 6y + 5 = 0\) và đường thẳng \(d: 2x+y-1=0\). Viết phương trình tiếp tuyến \(\Delta \) của \((C)\), biết \(\Delta \) song song với \(d\). Tìm tọa độ tiếp điểm. Giải \((C)\) có tâm \(I(1 ; -3)\), bán kính \(R = \sqrt {{1^2} + {3^2} - 5} = \sqrt 5 \). \(\Delta //d \Rightarrow \Delta \) có phương trình : \(2x + y + m = 0 (m \ne - 1)\). \(\Delta \) tiếp xúc với \((C)\) \( \Leftrightarrow d(I ; \Delta ) = R \\ \Leftrightarrow \dfrac{{|2 - 2 + m|}}{{\sqrt {{2^2} + {1^2}} }} = \sqrt 5 \\ \Leftrightarrow |m - 1| = 5 \\ \Leftrightarrow \left[ \begin{array}{l}m = 6\\m = - 4.\end{array} \right.\) Có hai tiếp tuyến cần tìm là : \(\begin{array}{l}{\Delta _1}: 2x + y + 6 = 0;\\{\Delta _2}: 2x + y - 4 = 0.\end{array}\) Tọa độ tiếp điểm \(M\) của \({\Delta _1}\) với \((C)\) là nghiệm của hệ \(\left\{ \begin{array}{l}2x + y + 6 = 0\\{x^2} + {y^2} - 2x + 6y + 5 = 0\end{array} \right. \) \( \Leftrightarrow \left\{ \begin{array}{l}x = - 1\\y = - 4\end{array} \right.\). Vậy \(M=(-1 ; -4).\) Tọa độ tiếp điểm N của \({\Delta _2}\) với \((C)\) là nghiệm của hệ \(\left\{ \begin{array}{l}2x + y - 4 = 0\\{x^2} + {y^2} - 2x + 6y + 5 = 0\end{array} \right. \) \( \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = - 2\end{array} \right.\). Vậy \(N=(3 ; -2).\) Sachbaitap.com
Xem thêm tại đây:
Bài 4. Đường tròn.
|

 Tải ngay
Tải ngay