Tải ngay
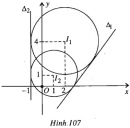
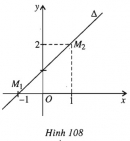
Bài 55 trang 108 SBT Hình học 10 Nâng caoGiải bài tập Bài 55 trang 108 SBT Hình học 10 Nâng cao Cho đường tròn \((C)\) có phương trình \({x^2} + {y^2} + 4x + 4y - 17 = 0\). Viết phương trình tiếp tuyến \(\Delta \) của \((C)\) trong mỗi trường hợp sau: a) \(\Delta \) tiếp xúc với \((C)\) tại \(M(2 ; 1);\) b) \(\Delta \) vuông góc với đường thẳng \(d: 3x-4y+1=0;\) c) \(\Delta \) đi qua \(A(2 ; 6).\) Giải a) \(\Delta : 4x + 3y - 11 = 0\). b) Có hai tiếp tuyến là \({\Delta _1}: 4x + 3y + 39 = 0\) và \({\Delta _2}: 4x + 3y - 11 = 0\). c) Có hai tiếp tuyến là : \({\Delta _1}: y = \dfrac{{ - 32 + 5\sqrt {55} }}{9}(x - 2) + 6 , \) \( {\Delta _2}: y = \dfrac{{ - 32 - 5\sqrt {55} }}{9}(x - 2) + 6\). Sachbaitap.com
Xem thêm tại đây:
Bài 4. Đường tròn.
|
