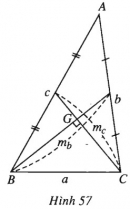
Bài 61 trang 48 SBT Hình học 10 Nâng caoGiải bài tập Bài 61 trang 48 SBT Hình học 10 Nâng cao Tam giác \(ABC\) có \(\dfrac{c}{b} = \dfrac{{{m_b}}}{{{m_c}}} \ne 1\). Chứng minh rằng: \(2\cot A = \cot B + \cot C\). Giải Đẳng thức \(2\cot A = \cot B + \cot C\) tương đương với \(2.\dfrac{{{b^2} + {c^2} - {a^2}}}{{abc}}R = \dfrac{{{a^2} + {c^2} - {b^2}}}{{abc}}R \) \(= \dfrac{{{a^2} + {b^2} - {c^2}}}{{abc}}R\) (theo tính toán như bài 58) hay \({b^2} + {c^2} = 2{a^2}\). Từ giả thiết suy ra \({c^2}m_c^2 = {b^2}m_b^2\), do đó \(\begin{array}{l}{c^2}\left( {\dfrac{{{b^2} + {a^2}}}{2} - \dfrac{{{c^2}}}{4}} \right) \\= {b^2}\left( {\dfrac{{{c^2} + {a^2}}}{2} - \dfrac{{{b^2}}}{4}} \right)\\ \Rightarrow 2{b^2}{c^2} + 2{a^2}{c^2} - {c^4}\\ = 2{b^2}{c^2} + 2{a^2}{b^2} - {b^4}.\\ \Rightarrow {b^4} - {c^4} = 2{a^2}({b^2} - {c^2})\end{array}\) \( \Rightarrow {b^2} + {c^2} = 2{a^2}.\) (do \({b^2} - {c^2} \ne 0\)). Ta đi đến điều phải chứng minh. Sachbaitap.com
Xem thêm tại đây:
Bài 3. Hệ thức lượng trong tam giác.
|

 Tải ngay
Tải ngay