Bài 63 trang 48 SBT Hình học 10 Nâng caoGiải bài tập Bài 63 trang 48 SBT Hình học 10 Nâng cao Chứng minh rằng hai trung tuyến kẻ từ \(B\) và \(C\) của tam giác \(ABC\) vuông góc với nhau khi và chỉ khi có hệ thức sau: \(\cot A = 2(\cot B + \cot C).\) Giải
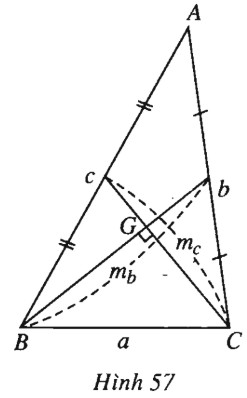
Gọi \(G\) là trọng tâm tam giác ABC (h.57). Khi đó \(GB \bot GC \Leftrightarrow {a^2} = \dfrac{4}{9}\left( {m_b^2 + m_c^2} \right)\) \(\begin{array}{l}\Leftrightarrow 9{a^2} = 4\left( {\dfrac{{{a^2} + {c^2}}}{2} - \dfrac{{{b^2}}}{4} + \dfrac{{{a^2} + {b^2}}}{2} - \dfrac{{{c^2}}}{4}} \right)\\ \Leftrightarrow 9{a^2} = 4{a^2} + {b^2} + {c^2}\\\Leftrightarrow 5{a^2} = {b^2} + {c^2}.\end{array}\) Biến đổi đẳng thức \(\cot A = 2\left( {\cot B + \cot C} \right)\) \( \Leftrightarrow \dfrac{{{b^2} + {c^2} - {a^2}}}{{abc}}R\) \(= 2\left( {\dfrac{{{a^2} + {c^2} - {b^2}}}{{abc}}R + \dfrac{{{a^2} + {b^2} - {c^2}}}{{abc}}R} \right)\) ( theo bài 58). \( \Leftrightarrow {b^2} + {c^2} = 5{a^2}\). Vậy \(GB \bot GC\) \(\Leftrightarrow \cot A = 2\left( {\cot B + \cot C} \right)\). Sachbaitap.com
Xem thêm tại đây:
Bài 3. Hệ thức lượng trong tam giác.
|

 Tải ngay
Tải ngay