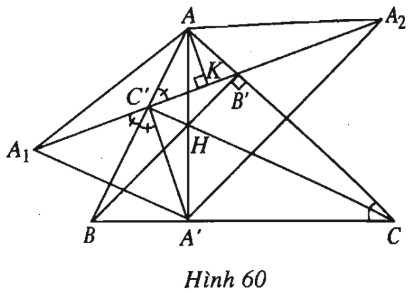
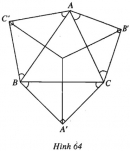
Bài 67 trang 49 SBT Hình học 10 Nâng caoGiải bài tập Bài 67 trang 49 SBT Hình học 10 Nâng cao Kẻ các đường cao \(AA’, BB’, CC’\) của tam giác nhọn \(ABC.\) a) Chứng minh rằng \(B'C' = 2R\sin A\cos A\). b) Lấy \(A_1, A_2\) lần lượt là điểm đối xứng với \(A’\) qua \(AB, AC\). Chứng minh rằng chu vi tam giác \(A’B’C’\) bằng độ dài đoạn thẳng \(A_1A_2\). c) Chứng minh hệ thức: \(\sin A\cos A + \sin B\cos B + \sin C\cos C \) \(= 2\sin A\sin B\sin C\). Giải (h.60).
a) Ta có \(AB’=AB\cos A=2R \sin C \cos A.\) Trong tam giác \(AB’C’\) có \(\dfrac{{B'C'}}{{\sin A}} = \dfrac{{AB'}}{{\sin C'}}\). Nhưng \(\widehat {AC'B'} = \widehat C\) (do \(BC’B’C\) là tứ giác nội tiếp), suy ra \(\dfrac{{B'C'}}{{\sin A}} = \dfrac{{AB'}}{{\sin C}}\). Từ đó suy ra \(B'C' = \dfrac{{AB'\sin A}}{{\sin C'}}\) \(= \dfrac{{2R\sin C\cos A\sin A}}{{\sin C}}\) \(= 2R\sin A\cos A\). b) Ta có \(\widehat {{A_1}C'B} = \widehat {BC'A'}\) (do \(A_1, A’\) đối xứng với nhau qua \(AB\)). \(\widehat {BC'A'} = \widehat {AC'B'}\) (do \(AC’A’C\) và \(BC’B’C\) cùng là tứ giác nội tiếp). Suy ra \(\widehat {{A_1}C'B} = \widehat {B'C'A}\). Vậy \(A_1, C’, B’\) thẳng hàng và \(A_1C’=A’C’.\) Tương tự cũng có \(C’, B’, A_2\) thẳng hàng và \(B’A_2=B’A’.\) Do đó, chu vi tam giác \(A’B’C’\) bằng \(A’C’+C’B’+B’A’\) \(=A_1C’+C’B’+B’A_2=A_1A_2\). c) Do \(A_1\) và \(A’\) đối xứng nhau qua \(AB\) nên \(A{A_1} = AA' , \widehat {{A_1}AB} = \widehat {BAA'}\); \(A_2\) và \(A’\) đối xứng nhau qua \(AC\) nên \(A{A_2} = AA' , \widehat {A'AC} = \widehat {CA{A_2}}\). Do đó tam giác \(AA_1A_2\)là tam giác cân có góc ở đỉnh \(\widehat {{A_1}A{A_2}} = 2\widehat A\). Kẻ \(AK\) vuông góc với \(A_1A_2\), ta có \(A_1A_2=2A_1K\) \(=2AA_1 \sin A=2AA’\sin A\) \(=2AB\sin B\sin A\) \(=4R\sin C\sin B\sin A.\) Mặt khác theo câu a), ta có \(B’C’+B’A’+A’C’\) \(=2R \sin A \cos A+2R \sin C \cos C\)\(+2R \sin B \cos B.\) Từ đó suy ra hệ thức cần chứng minh. Sachbaitap.com
Xem thêm tại đây:
Bài 3. Hệ thức lượng trong tam giác.
|

 Tải ngay
Tải ngay