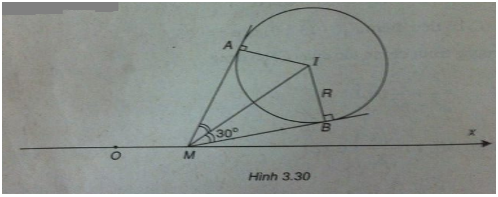
Bài 7 trang 197 Sách bài tập (SBT) Toán Hình học 10Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) : \({x^2} + {y^2} - 6x - 6y + 14 = 0\). Tìm điểm M thuộc trục hoành sao cho từ M kẻ được hai tiếp tuyến của (C) mà góc giữa hai tiếp tuyến đó bằng \({60^ \circ }\). Gợi ý làm bài (Xem hình 3.30)
Đường tròn (C) có tâm I(3 ; 3) và có bán kính \(R = \sqrt {{a^2} + {b^2} - c} = \sqrt {9 + 9 - 14} = 2\) Điểm M(x;0) thuộc Ox. Từ M kẻ hai tiếp tuyến tiếp xúc với (C) tại A và B. Ta có: \(\widehat {AMB} = {60^ \circ } \Rightarrow \widehat {IMB} = {30^ \circ }\) \( \Rightarrow IM = {R \over {\sin {{30}^ \circ }}} = 2R = 4\) \(IM = 4 \Leftrightarrow \sqrt {{{\left( {x - 3} \right)}^2} + 9} = 4\) \( \Leftrightarrow {x^2} - 6x + 2 = 0\) \( \Leftrightarrow x = 3 \pm \sqrt 7 \) Vậy có hai điểm M thỏa mãn đề bài, chúng có tọa độ là : \({M_1}\left( {3 + \sqrt 7 ;0} \right)\) và \({M_2}\left( {3 - \sqrt 7 ;0} \right)\) Sachbaitap.net
Xem lời giải SGK - Toán 10 - Xem ngay >> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
Xem thêm tại đây:
I-Đề toán tổng hợp
|

 Tải ngay
Tải ngay