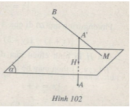
Bài 73 trang 134 Sách bài tập Hình học lớp 12 Nâng cao

a) Tìm tọa độ điểm đối xứng của M₀(2;-3;1) qua mặt phẳng \(\left( \alpha  \right):x + 3y - z + 2 = 0.\)

b) Tìm tọa độ điểm đối xứng của A(0;0;1) qua mặt phẳng

\(6x + 3y + 2z - 6 = 0.\)

c) Tìm tọa độ điểm đối xứng của B(2;3;5) qua mặt phẳng

\(2x + 3y + z - 17 = 0.\)

Giải

a) Trước hết, ta xác định hình chiếu vuông góc H của M₀ trên (\(\alpha \)). Gọi d là đường thẳng qua M₀ và vuông góc với (\(\alpha \)), ta có

                             \(d:\left\{ \matrix{  x = 2 + t \hfill \cr  y =  - 3 + 3t \hfill \cr  z = 1 - t. \hfill \cr}  \right.\)

Toạ độ điểm H(x; y; z) thoả mãn hệ :

            \(\left\{ \matrix{  x = 2 + t \hfill \cr  y =  - 3 + 3t \hfill \cr  z = 1 - t \hfill \cr  x + 3y - z + 2 = 0 \hfill \cr}  \right. \Rightarrow H = \left( {{{28} \over {11}}; - {{15} \over {11}};{5 \over {11}}} \right).\)

Gọi M' là điểm đối xứng của M₀ qua mặt phẳng (\(\alpha \)) thì H là trung điểm của M₀M' nên ta có :

             \(\left\{ \matrix{  {{{x_{M'}} + 2} \over 2} = {{28} \over {11}} \hfill \cr  {{{y_{M'}} - 3} \over 2} =  - {{15} \over {11}} \hfill \cr  {{{z_{M'}} + 1} \over 2} = {5 \over {11}} \hfill \cr}  \right. \Rightarrow M' = \left( {{{34} \over {11}};{3 \over {11}}; - {1 \over {11}}} \right).\)

Tương tự

b) \(A' = \left( {{{48} \over {49}};{{24} \over {49}};{{65} \over {49}}} \right).\)

c) \(B' = \left( {{{12} \over 7};{{18} \over 7};{{34} \over 7}} \right).\)

Sachbaitap.com