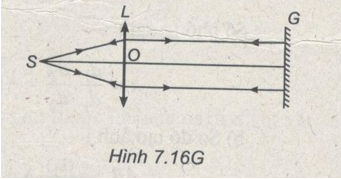
Bài 7.37 trang 87 Sách bài tập (SBT) Vật lí 11 Nâng cao

Bài 7.37 trang 87 Sách bài tập (SBT) Vật lí 11 nâng cao

Một thấu kính hội tụ L có một mặt phẳng và một mặt lồi bán kính R = 1 m. Chiết suất của thấu kính n = 1,5. Một điểm sáng S ở trên trục chính, cách L 2 m. Đặt một gương phẳng G vuông góc với trục chính của L, cách L là 7 m.

a) Chứng tỏ rằng ảnh cuối cùng của S cho bởi quang hệ có vị trí trùng với S.

b) Giữ nguyên vị trí của S và gương phẳng G. Hỏi có vị trí nào khác của thấu kính L trong khoảng từ S tới gương để ảnh cuối cùng của S cũng trùng với S ?

Giải :

a) Tiêu cự của L : \({1 \over f} = \left( {n - 1} \right)\left( {{1 \over {{R_1}}} + {1 \over {{R_2}}}} \right)\)

với \({R_1} = \infty ,{R_2} = R = 1m,n = 1,5\), ta tính được \(f = 2m\).

Vậy điểm sáng S trùng với tiêu điểm F của L. Chùm tia ló khỏi L có phương song song với trục chính nên tới thẳng góc với gương phẳng G. Các tia phản xạ trùng với các tia tới gương nên khi ló ra khỏi L sẽ đi qua S (Hình 7.16G).

Vậy ảnh cuối cùng trùng với S.

b) Gọi \({d_1}\) là khoảng cách từ S tới thấu kính L. Sơ đồ tạo ảnh như sau :

\({S_{{d_1}}}{\buildrel {\left( L \right)} \over
\longrightarrow _{d{'_1}}}{S_{{1_{{d_2}}}}}{\buildrel {\left( G \right)} \over
\longrightarrow _{d{'_2}}}{S_{{2_{{d_3}}}}}{\buildrel {\left( L \right)} \over
\longrightarrow _{d{'_3}}}{S_3}\)

Ta có: \({1 \over f} = {1 \over {{d_1}}} + {1 \over {d{'_1}}}\)

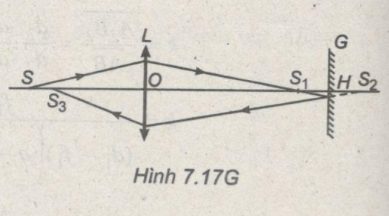
Với chùm tia phản xạ (từ gương G) đi qua L (Hình 7.17G), ta có :

\({1 \over f} = {1 \over {{d_3}}} + {1 \over {d{'_3}}}\)

Nếu \({S_3}\) trùng với S, ta có \(d{'_3} = {d_1}\), suy ra: \({d_3} = d{'_1}\) hay \({S_2} \equiv {S_1} \equiv H\).

Ta có: \({d_1} + d{'_1} = SH = 9m\) hay \({d_1} + {{{d_1}f} \over {{d_1} - f}} = 9\).

Từ đó ta có phương trình : 

\(d_1^2 - 9{d_1} + 18 = 0\)

Giải phương trình, ta tìm được hai nghiệm là :

\({d_1} = 6m\) và \({d_1} = 3m\)

Vậy phải đặt L cách S là 6 m hoặc 3 m.

Sachbaitap.com