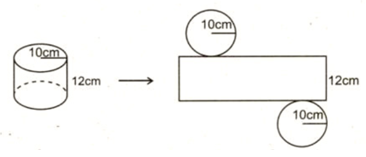
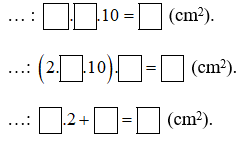Bài 8, 9, 10, 11, 12, 13, 14 trang 111, 112, 113 SGK Toán 9 tập 2 - Luyện tậpGiải bài 8 trang 111; bài 9, 10, 11, 12 trang 112; bài 13, 14 trang 113 sách giáo khoa (SGK) Toán lớp 9 tập 2 bài Luyện tập. Bài 13 Một tấm kim loại được khoan thủng bốn lỗ như hình 85 (lỗ khoan dạng hình trụ),tấm kim loại dày 2cm, đáy của nó là hình vuông cạnh là 5 cm. Bài 8 trang 111 SGK Toán lớp 9 tập 2 Câu hỏi: Cho hình chữ nhật \(ABCD\) \((AB = 2a, BC = a).\) Quay hình chữ nhật đó quanh \(AB\) thì được hình trụ có thể tích \({V_1}\); quanh \(BC\) thì được hình trụ có thể tích \({V_2}\). Trong các đẳng thức sau đây, hãy chọn đẳng thức đúng. (A) \({V_1} = {V_2}\); (B) \({V_1} = 2{V_2}\); (C) \({V_2} = 2{V_1}\) (D) \({V_2} =3 {V_1}\) (E) \({V_1} = 3{V_2}\). Lời giải: Quay quanh \(AB\) thì ta được hình trụ có \(r =BC= a, \, h= AB=2a.\) \(\Rightarrow {V_1} = \pi {r^2}h = \pi {a^2}.2a = 2\pi {a^3}.\) Quay quanh \(BC\) thì ta được hình trụ có \(r =AB= 2a, \, h =BC= a.\) \(\Rightarrow {V_2} = \pi {r^2}h = \pi {{(2a)}^2}.a = 4\pi {a^3}.\) Do đó \({V_2} = 2{V_1}\) Vậy chọn C. Bài 9 trang 112 SGK Toán lớp 9 tập 2 Câu hỏi: Hình 83 là mình hình trụ cùng với hình khai triển của nó kèm theo kích thước.
Hãy điền vào các chỗ trống ... và các ô trống trong những cụm từ hoặc các số cần thiết.
Lời giải: Diện tích đáy là: \(10.\pi .10 = 100\pi (c{m^2}).\) Diện tích xung quanh là: \((2.\pi .10).12 = 240\pi {cm^2}).\) Diện tích toàn phần: \(100\pi .2 + 240\pi = 440\pi (c{m^2}).\) Bài 10 trang 112 SGK Toán lớp 9 tập 2 Câu hỏi: Hãy tính: a) Diện tích xung quanh của một hình trụ có chu vi hình tròn đáy là \(13cm\) và chiều cao là \(3cm.\) b) Thể tích hình trụ có bán kính đường tròn đáy là \(5 mm\) và chiều cao là \(8 mm.\) Phương pháp: +) Diện tích xung quanh hình trụ: \(S_{xq}=C.h=2\pi rh.\) +) Thể tích hình trụ: \(V=\pi r^2.h.\) Lời giải: a) Ta có: \(C = 13cm, \, h = 3cm\) Diện tích xung quanh của hình trụ là: \({S_{xq}} = 2\pi rh = C.h = 13.3 = 39(c{m^2}).\) b) Ta có \(r = 5 mm , \, h = 8mm\) Thể tích của hình trụ là: \(V = \pi {r^2}h = \pi {5^2}.8 = 200\pi (m{m^3})\). Bài 11 trang 112 SGK Toán lớp 9 tập 2 Câu hỏi: Người ta nhấm chìm hoàn toàn một tượng đã nhỏ vào một lọ thủy tinh có nước dạng hình trụ (h84). Diện tích đáy lọ thủy tinh là \(12,8 \, cm^2.\) Nước trong lọ dâng lên \(8,5 \, mm.\) Hỏi thể tích của tượng đá là bao nhiêu?
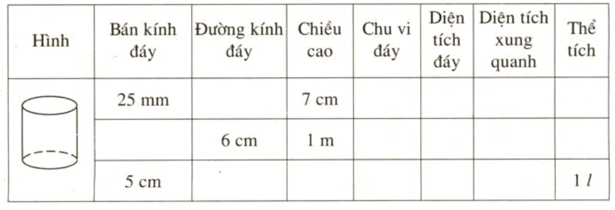
Phương pháp: +) Thể tích của hình trụ: \(V=Sh=\pi r^2h.\) Lời giải: Do thể tích tượng bằng thể tích nước dâng lên nên thể tích của tượng đá bằng thể tích của hình trụ có diện tích đáy là \(12,8\) \(cm^2\) và chiều cao bằng \(8,5 mm=0,85 cm.\) Vậy: \(V = S.h = 12,8.0,85 = 10,88\) \(cm^3.\) Bài 12 trang 112 SGK Toán lớp 9 tập 2 Câu hỏi: Điền đủ các kết quả vào những ô trống của bảng sau:
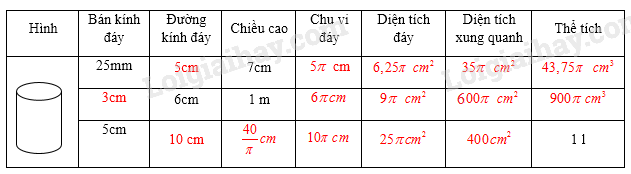
Lời giải: Đổi \(25mm = 2,5cm;1m = 100cm;1l = 1000c{m^3}\) + Khi \(r = 2,5cm;h = 7cm\) thì hình trụ có - Đường kính \(d = 2r = 2.2,5 = 5cm\) - Chu vi đáy \(C = 2\pi r = 2.\pi .2,5 = 5\pi \left( {cm} \right)\) - Diện tích đáy \(S = \pi {r^2} = \pi .2,{5^2} = 6,25\pi \left( {c{m^2}} \right)\) - Diện tích xung quanh \({S_{xq}} = 2\pi rh = 2\pi .2,5.7 = 35\pi \left( {c{m^2}} \right)\) - Thể tích \(V = \pi {r^2}h = \pi .2,{5^2}.7 = 43,75\pi \left( {c{m^3}} \right)\) + Khi \(d = 6cm;h = 100cm\) thì hình trụ có - Bán kính \(r = \dfrac{d}{2} = \dfrac{6}{2} = 3cm\) - Chu vi đáy \(C = 2\pi r = 2.\pi .3 = 6\pi \left( {cm} \right)\) - Diện tích đáy \(S = \pi {r^2} = \pi {.3^2} = 9\pi \left( {c{m^2}} \right)\) - Diện tích xung quanh \({S_{xq}} = 2\pi rh = 2\pi .3.100 = 600\pi \left( {c{m^2}} \right)\) - Thể tích \(V = \pi {r^2}h = \pi {.3^2}.100 = 900\pi \left( {c{m^3}} \right)\) + Khi \(r = 5cm;V = 1000c{m^3}\) thì hình trụ có - Đường kính \(d = 2r = 2.5 = 10cm\) - Chu vi đáy \(C = 2\pi r = 2.\pi .5 = 10\pi \left( {cm} \right)\) - Diện tích đáy \(S = \pi {r^2} = \pi {.5^2} = 25\pi \left( {c{m^2}} \right)\) - Chiều cao \(h = \dfrac{V}{{\pi {r^2}}} = \dfrac{{1000}}{{\pi {{.5}^2}}} = \dfrac{{40}}{\pi }\left( {cm} \right)\) - Diện tích xung quanh \({S_{xq}} = 2\pi rh = 2\pi .5.\dfrac{{40}}{\pi } = 400\left( {c{m^2}} \right)\) Ta có bảng sau:
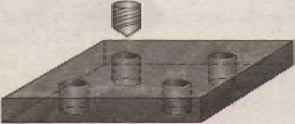
Bài 13 trang 113 SGK Toán lớp 9 tập 2 Câu hỏi: Một tấm kim loại được khoan thủng bốn lỗ như hình 85 (lỗ khoan dạng hình trụ), tấm kim loại dày \(2 cm,\) đáy của nó là hình vuông có cạnh \(5cm.\) Đường kính của mũi khoan là \(8mm.\) Hỏi thể tích phần còn lại của tấm kim loại là bao nhiêu?
Lời giải: Bán kính đáy của hình trụ (lỗ khoan) \(4mm\). Chiều cao của hình trụ là bề dày của tấm kim loại dày 2 cm = 20 mm Thể tích một lỗ khoan hình trụ là: \({V_1} = π.4^2.20 ≈ 1005\) \((mm^3)=1,005 \,cm^3.\) Thể tích của bốn lỗ khoan là \({V_4} = 4{V_1}≈4. 1,005= 4,02\) (\(cm^3\)). Thể tích của tấm kim loại là: \(V = 5.5.2 = 50\) (\(cm^3.\)) Vậy thể tích phần còn lại của tấm kim loại là: \( V'=V-V_4=50-4,02=45,98 \, cm^3.\) Bài 14 trang 113 SGK Toán lớp 9 tập 2 Câu hỏi: Đường ống nối hai bể cá trong một thủy cung ở nam nước Pháp có dạng hình trụ, độ dài của đường ống là \(30m\) ( h86). Dung tích của đường ống nói trên là \(1 800 000\) lít. Tính diện tích đáy của đường ống.
Phương pháp: Cho hình trụ có các kích thước: chiều cao là \(h,\) bán kính đáy là \(r.\) Khi đó: Thể tích của hình trụ là: \(V=Sh=\pi r^2 h.\) Lời giải: Thể tích của đường ống là: \(V = 1 800 000\) lít \(= 1 800 000 dm^3 = 1800 m^3.\) Chiều cao của hình trụ là: \(h = 30 m.\) Vì \(V= Sh \Rightarrow S = \dfrac{V}{h}= \dfrac{1800}{30} = 60\) \((m^2).\) Vậy diện tích đáy của đường ống là 60 \(m^2\) Sachbaitap.com
Xem thêm tại đây:
Bài 1. Hình trụ - Diện tích xung quanh và thể tích hình trụ
|
-

Bài 15, 16, 17, 18 trang 117 SGK Toán 9 tập 2 - Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt
Giải bài 15, 16, 17, 18 trang 117 sách giáo khoa (SGK) Toán lớp 9 tập 2 bài Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt. Bài 17 Khi quay tam giác vuông để tạo ra một hình nón như hình 87 thì góc CAO gọi là nửa góc ở đỉnh của hình nón. Biết nửa góc ở đỉnh của một hình nón là 30°, độ dài đường sinh là a.
-
Bài 19, 20, 21, 22 trang 118 SGK Toán 9 tập 2 - Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt
Giải bài 19, 20, 21, 22 trang 118 sách giáo khoa (SGK) Toán lớp 9 tập 2 bài Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt. Bài 21 Cái mũ của chú hề với các kích thước cho theo hình vẽ (h.97). Hãy tính tổng diện tích vải cần có để làm nên cái mũ (không kể riềm, mép, phần thừa)
-

Bài 23, 24, 25, 26, 27, 28, 29 trang 119, 120 SGK Toán 9 tập 2 - Luyện tập
Giải bài 23, 24, 25, 26, 27 trang 119; bài 28, 29 trang 120 sách giáo khoa (SGK) Toán lớp 9 tập 2 bài Luyện tập. Bài 27 Một dụng cụ gồm một phần có dạng hình trụ, phần còn lại có dạng hình nón. Các kích thước cho trên hình 100.

 Tải ngay
Tải ngay