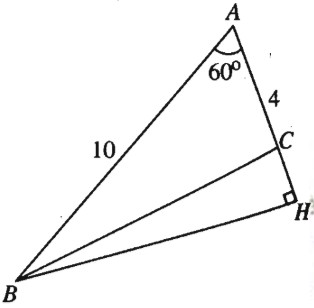
Bài 87 trang 51 SBT Hình học 10 Nâng caoGiải bài tập Bài 87 trang 51 SBT Hình học 10 Nâng cao Biết rằng tam giác \(ABC\) có \(AB=10, AC=4\) và \(\widehat A = {60^0}\). a) Tính chu vi của tam giác. b) Tính \(\tan C.\) c) Lấy điểm \(D\) trên tia đối của tia \(AB\) sao cho \(AD=6\) và điểm \(E\) trên tia \(AC\) sao cho \(AE=x\). Tìm \(x\) để \(BE\) là tiếp tuyến của đường tròn \((ADE)\) (\((ADE)\) là đường tròn ngoại tiếp tam giác \(ADE\)). Giải a) Ta đi tìm độ dài cạnh \(BC\). Áp dụng định lí cosin, ta có \(B{C^2} = {10^2} + {4^2} - 2.4.10.\cos {60^0} = 76\) Suy ra \(BC \approx 8,72\). Chu vi tam giác \(2p \approx 10 + 4 + 8,72 \approx 22,72\). b) (h.73).
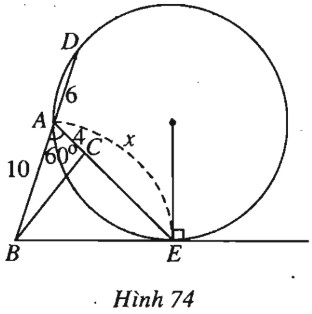
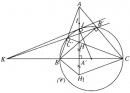
Kẻ đường cao \(BH\) ta có \(AH = AB. \cos {60^0} = 5\), suy ra \(HC=5-4=1.\) \(BH = AB.\sin {60^0} = 5\sqrt 3 ,\) \( \tan C = - \tan \widehat {BCH} = - \dfrac{{HB}}{{HC}}\)\( = - 5\sqrt 3 \). c) (h.74).
Để \(BE\) là tiếp tuyến của đường tròn \((ADE)\) phải có \(B{E^2} = BA.BD = 10(10 + 6) = 160\). Ta có \(AE = x\), áp dụng định lí cosin cho tam giác \(ABE\) : \(B{E^2} = {x^2} + 100 - 10x\). Từ đó có phương trình: \({x^2} - 10x + 100 - 160\) hay \({x^2} - 10 - 60 = 0\), phương trình này có một nghiệm dương là \(x = 5 + \sqrt {85} \). Vậy điểm \(E\) cần tìm là điểm trên tia \(AC\) và cách \(A\) một khoảng bằng \(5 + \sqrt {85} \). Sachbaitap.com
Xem thêm tại đây:
Bài tập Ôn tập chương II - Tích vô hướng của hai vectơ và ứng dụng
|

 Tải ngay
Tải ngay