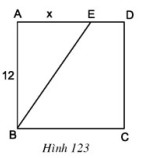
Bài 9, 10, 11, 12, 13, 14, 15 trang 118, 119 SGK Toán 8 tập 1 - Luyện tậpBài 9, 10, 11, 12, 13, 14, 15 trang 118, 119 SGK Toán 8 tập 1 - Luyện tập. Bài 14 Một đám đất hình chữ nhật dài \(700m\), rộng \(400m\). Hãy tính diện tích đám đất đó theo đơn vị \({m^2},k{m^2},a,ha\). Bài 9 trang 118 SGK Toán lớp 8 tập 1 Câu hỏi: \(ABCD\) là một hình vuông cạnh \( 12cm\), \(AE = x(cm)\) (h.\(123\)). Tính \(x\) sao cho diện tích tam giác \(ABE\) bằng \(\dfrac{1}{3}\) diện tích hình vuông \(ABCD\).
Phương pháp: Áp dụng: +) Công thức tính diện tích tam giác vuông: Diện tích tam giác vuông bằng nửa tích của hai cạnh góc vuông. +) Công thức tính diện tích hình vuông: Diện tích hình vuông bằng bình phương cạnh của nó. Lời giải:
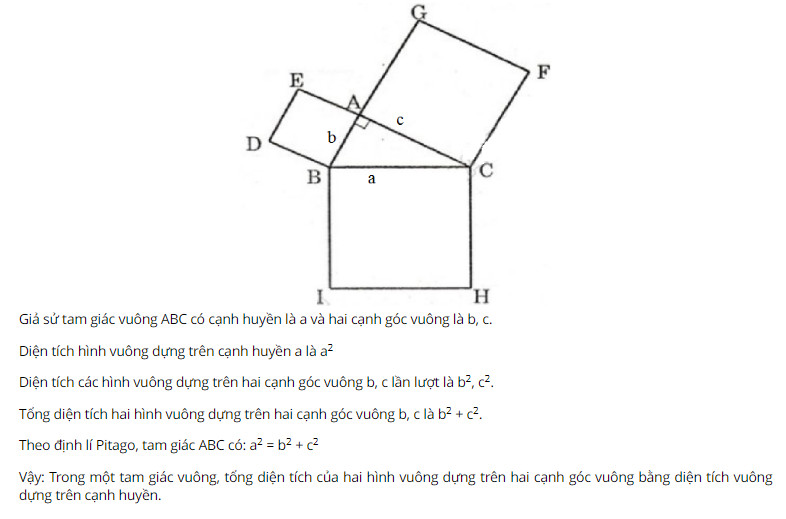
Bài 10 trang 118 SGK Toán lớp 8 tập 1 Câu hỏi: Cho một tam giác vuông. Hãy so sánh tổng diện tích của hai hình vuông dựng trên hai góc vuông với diện tích hình vuông dựng trên cạnh huyền. Phương pháp: - Áp dụng công thức tính diện tích hình vuông: Diện tích hình vuông bằng bình phương độ dài 1 cạnh. - Định lí Pytago: Bình phương cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông. Lời giải:
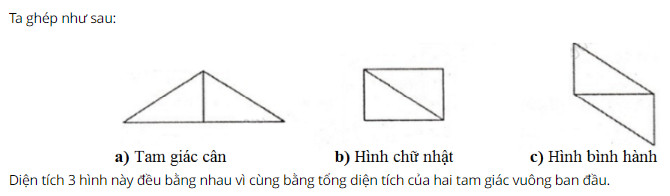
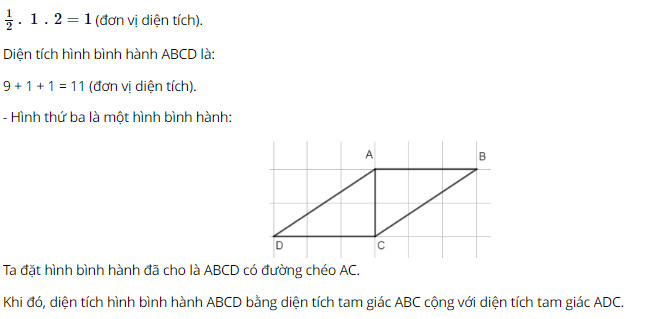
Bài 11 trang 118 SGK Toán lớp 8 tập 1 Câu hỏi: Cắt hai tam giác vuông bằng nhau từ một tấm bìa. Hãy ghép hai tam giác đó để tạo thành: a) Một tam giác cân; b) Một hình chữ nhật; c) Một hình bình hành. Diện tích các hình này có bằng nhau không? Vì sao? Phương pháp: Áp dụng tính chất diện tích đa giác: - Hai tam giác bằng nhau thì có diện tích bằng nhau. - Nếu một đa giác được chia thành những đa giác không có điểm trong chung thì diện tích của nó bằng tổng diện tích của những đa giác đó. Lời giải:
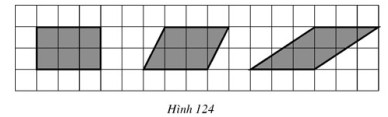
Bài 12 trang 118 SGK Toán lớp 8 tập 1 Câu hỏi: Tính diện tích các hình dưới đây (h.\(124\)) (mỗi ô vuông là \(1\) đơn vị diện tích)
Phương pháp: Áp dụng công thức tính diện tích: + Diện tích tam giác vuông bằng nửa tích hai cạnh góc vuông. + Diện tích hình chữ nhật bằng tích của chiều dài và chiều rộng + Diện tích hình vuông cạnh \(a\) bằng \(a^2\) Lời giải:
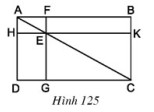
Bài 13 trang 118 SGK Toán lớp 8 tập 1 Câu hỏi: Cho hình \(125\), trong đó \(ABCD\) là hình chữ nhật, \(E\) là một điểm bất kì nằm trên đường chéo \(AC, FG // AD\), và \(HK // AB\). Chứng minh rằng hai hình chữ nhật \(EFBK\) và \(EGDH\) có cùng diện tích.
Phương pháp: Áp dụng tính chất: Hai tam giác bằng nhau thì có diện tích bằng nhau. Lời giải:
Bài 14 trang 118 SGK Toán lớp 8 tập 1 Câu hỏi: Một đám đất hình chữ nhật dài \(700m\), rộng \(400m\). Hãy tính diện tích đám đất đó theo đơn vị \({m^2},k{m^2},a,ha\). Phương pháp: Áp dụng công thức tính diện tích hình chữ nhật, qui tắc đổi đơn vị diện tích. \(1k{m^2} = 1000000\,({m^2})\), \(1\,a=100m^2,1\,ha=10000m^2\) Lời giải:
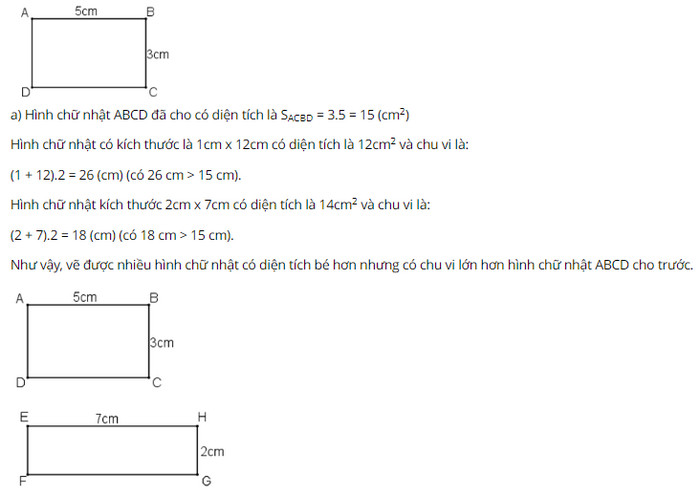
Bài 15 trang 118 SGK Toán lớp 8 tập 1 Câu hỏi: Đố. Vẽ hình chữ nhật \(ABCD\) có \(AB = 5\,cm, BC = 3\,cm.\) a) Hãy vẽ một hình chữ nhật có diện tích nhỏ hơn nhưng có chu vi lớn hơn hình chữ nhật \(ABCD.\) Vẽ được mấy hình như vậy. b) Hãy vẽ hình vuông có chu vi bằng chu vi hình chữ nhật \(ABCD.\) Vẽ được mấy hình vuông như vậy? So sánh diện tích hình chữ nhật với diện tích hình vuông có cùng chu vi vừa vẽ. Tại sao trong các hình chữ nhật có cùng chu vi thì hình vuông có diện tích lớn nhất. Phương pháp: Áp dụng công thức tính diện tích hình chữ nhật, diện tích hình vuông. Lời giải:
Sachbaitap.com
Xem thêm tại đây:
Chương II: Đa giác. Diện tích đa giác
|
-

Bài 6, 7, 8 trang 118 SGK Toán 8 tập 1 - Diện tích hình chữ nhật
Bài 6, 7, 8 trang 118 SGK Toán 8 tập 1 - Diện tích hình chữ nhật. Bài 7 Một gian phòng có nền hình chữ nhật với kích thước là (4,2,m) và (5,4,m) có một cửa sổ hình chữ nhật kích thước là (1,m) và (1,6,m) và một cửa ra vào hình chữ nhật kích thước là (1,2,m) và (2,m.)
-

Bài 16, 17, 18 trang 121 SGK Toán 8 tập 1 - Diện tích tam giác
Bài 16, 17, 18 trang 121 SGK Toán 8 tập 1 - Diện tích tam giác. Bài 18 Cho tam giác (ABC) và đường trung tuyến (AM) (h.(132)). Chứng minh rằng:
-

Bài 19, 20, 21, 22, 23, 24, 25 trang 121 SGK Toán 8 tập 1 - Luyện tập
Bài 19, 20, 21, 22 trang 122, bài 23, 24, 25 trang 123 SGK Toán 8 tập 1 - Luyện tập. Bài 25 Tính diện tích của một tam giác đều có cạnh là (a.)
-

Bài 26, 27, 28, 29, 30, 31 trang 125, 126 SGK Toán 8 tập 1 - Diện tích hình thang
Bài 26, 27 trang 125, bài 28, 29, 30, 31 trang 126 SGK Toán 8 tập 1 - Diện tích hình thang. Bài 27 Vì sao hình chữ nhật (ABCD) và hình bình hành (ABEF) (h.(141)) lại có cùng diện tích? Suy ra cách vẽ một hình chữ nhật có cùng diện tích với một hình bình hành cho trước.

 Tải ngay
Tải ngay