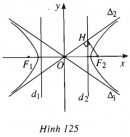
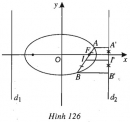
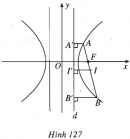
Bài 94 trang 120 SBT Hình học 10 Nâng caoGiải bài tập Bài 94 trang 120 SBT Hình học 10 Nâng cao Xác định tọa độ tiêu điểm, phương trình đường chuẩn của các cônic sau: a) \( \dfrac{{{x^2}}}{8} + \dfrac{{{y^2}}}{4} = 1;\) b) \( \dfrac{{{x^2}}}{{15}} - \dfrac{{{y^2}}}{{20}} = 1;\) c) \({y^2} = 6x.\) Giải a) Đây là elip có \({c^2} = {a^2} - {b^2} = 4 \Rightarrow c = 2\), ta có các tiêu điểm : \({F_1}( - 2 ; 0) , {F_2}(2 ; 0)\), các đường chuẩn: \(x = \pm \dfrac{{{a^2}}}{c} = \pm 4\). b) Đây là hypebol có \({c^2} = {a^2} + {b^2} = 35 \Rightarrow c = \sqrt {35} \), ta có tiêu điểm : \({F_1}( - \sqrt {35} ; 0), {F_2}(\sqrt {35} ; 0)\), các đường chuẩn : \(x = \pm \dfrac{{{a^2}}}{c} = \pm \dfrac{{15}}{{\sqrt {35} }}\). c) Đây là parabol có p=3, ta có tiêu điểm : \(F\left( { \dfrac{3}{2} ; 0} \right)\), đường chuẩn: \(x = - \dfrac{3}{2}\). Sachbaitap.com
Xem thêm tại đây:
Bài 8. Ba đường cônic.
|

 Tải ngay
Tải ngay