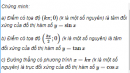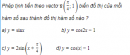Câu 1.13 trang 9 sách bài tập Đại số và Giải tích 11 Nâng caoCho biết đồ thị (h.1.3) sau Cho biết đồ thị (h.1.3) sau là đồ thị hàm số \(y = A\sin \left( {x + \alpha } \right) + B\) (\(A,B,\alpha \) là những hằng số). Hãy xác định \(A,B,\alpha \).
Giải Hàm số \(y = A\sin \left( {x + \alpha } \right) + B\) đạt giá trị lớn nhất là 3 tại \(x = {\pi \over 6}\) (coi \(A > 0\)) nên: \(\left\{ \matrix{ Hàm số \(y = A\sin \left( {x + \alpha } \right) + B\) đạt giá trị nhỏ nhất là -1 tại \(x = - {{5\pi } \over 6}\) nên: \(\left\{ \matrix{ Từ đó \(B = 1,A = 2\) và chú ý rằng \(\sin \left( { - {{5\pi } \over 6} + \alpha } \right) = \sin \left( {{\pi \over 6} + \alpha - \pi } \right) = \sin \left( {{\pi \over 6} + \alpha } \right)\) Nên chỉ cần chọn \(\alpha \) sao cho \(\left( {{\pi \over 6} + \alpha } \right) = 1,\) chẳng hạn \(\alpha = {\pi \over 3}\) Vậy \(A = 2,B = 1,\alpha = {\pi \over 3}\) sachbaitap.com
Xem lời giải SGK - Toán 11 Nâng cao - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Bài 1: Các hàm số lượng giác
|
-
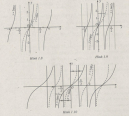
Câu 1.16 trang 9 sách bài tập Đại số và Giải tích 11 Nâng cao
Từ đồ thị của hàm số hãy suy ra đồ thị các hàm số sau:

 Tải ngay
Tải ngay