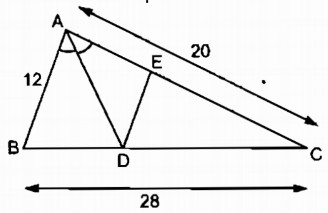
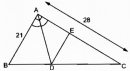
Câu 20 trang 87 Sách bài tập (SBT) Toán 8 tập 2Tính độ dài đoạn thẳng BD, DC và DE Tam giác ABC có AB = 12cm, AC = 20cm, BC = 28cm. Đường phân giác góc A cắt BC tại D. Qua D kẻ DE // AB (E thuộc AC) a. Tính độ dài đoạn thẳng BD, DC và DE b. Cho biết diện tích tam giác ABC là S, tính diện tích các tam giác ABD, ADE và DCE.
Giải: a. Trong tam giác ABC, ta có: AD là đường phân giác của \(\widehat {BAC}\) Suy ra: \({{DB} \over {DC}} = {{AB} \over {AC}}\) (tính chất tia phân giác) Suy ra: \({{DB} \over {DB + DC}} = {{AB} \over {AB + AC}}\) Suy ra: \({{DB} \over {BC}} = {{AB} \over {AB + AC}}\) Suy ra: \(DB = {{BC.AB} \over {AB + AC}} = {{28.12} \over {12 + 20}} = {{21} \over 2} = 10,5\) (cm) Vậy DC = BC – DB = 28 – 10,5 = 17,5 (cm) Trong tam giác ABC, ta có: DE // AB Suy ra: \({{DC} \over {BC}} = {{DE} \over {AB}}\) (Hệ quả định lí Ta-lét ) Vậy: \(DE = {{DC.AB} \over {BC}} = {{17,5.12} \over {28}} = 7,5\) (cm0 b. Vì ∆ABD và ∆ABC có chung đường cao kẻ từ đỉnh A nên: \({{{S_{ABD}}} \over {{S_{ABC}}}} = {{DB} \over {BC}} = {{{{21} \over 2}} \over {28}} = {{21} \over {56}} = {3 \over 8}\) Vậy : \({S_{ABD}} = {3 \over 8}S\) \({S_{ADC}} = {S_{ABC}} - {S_{ABD}} = S - {3 \over 8}S = {8 \over 8}S - {3 \over 8}S = {5 \over 8}S\) Vì DE // AB và AD là đường phân giác góc A nên AE = DE. Ta có: \({{{S_{ADE}}} \over {{S_{ADC}}}} = {{AE} \over {AC}} = {{DE} \over {AC}} = {{7,5} \over {20}}\) Vậy: \({S_{ADE}} = {{7,5} \over {20}}.{S_{ADC}} = {{7,5} \over {20}}.{5 \over 8}S = {{7,5} \over {32}}S\) Ta có: \({S_{DCE}} = {S_{ADC}} - {S_{ADE}} = {5 \over 8}S - {{7,5} \over {32}}S = {{12,5} \over {32}}S\). Sachbaitap.com
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 3. Tính chất đường phân giác của tam giác
|
-
Câu 24 trang 88 Sách bài tập (SBT) Toán 8 tập 2
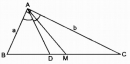
Tính độ dài các đoạn thẳng BC, BD, DC, AM và DM theo a, b.

 Tải ngay
Tải ngay