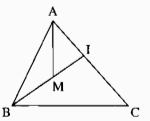
Câu 21 trang 40 Sách Bài Tập (SBT) Toán lớp 7 tập 2Chứng minh rằng MA + MB < IA + IB < CA + CB. Cho hình dưới. Chứng minh rằng MA + MB < IA + IB < CA + CB
Giải Trong ∆AMI ta có: MA < MI + IA (bất đẳng thức tam giác) Cộng vào 2 vế bất đẳng thức với MB ta có: MA + MB < MI + IA + MB \( \Rightarrow \) MA + MB < IB + IA (1) Trong ∆BIC ta có: IB < IC + CB (bất đẳng thức tam giác) Cộng vào 2 vế bất đẳng thức với IA ta có: IB + IA < IC + CB + IA \( \Rightarrow \) IB + IA < CA + CB (2) Từ (1) và (2) suy ra: MA + MB < IB + IA < CA + CB Sachbaitap.com
Xem lời giải SGK - Toán 7 - Xem ngay >> Học trực tuyến lớp 7 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 7 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
|
-
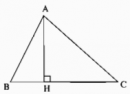
Câu 23 trang 40 Sách Bài Tập (SBT) Toán lớp 7 tập 2
a) Vì sao các góc B và C không thể là góc vuông hoặc góc tù?
-
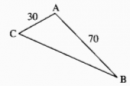
Câu 25 trang 41 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Nếu đặt ở C máy phát sóng truyền thanh có bán kính hoạt động bằng 40km thì thành phố B có nhận được tín hiệu không?

 Tải ngay
Tải ngay