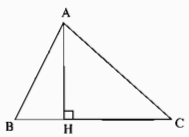
Câu 23 trang 40 Sách Bài Tập (SBT) Toán lớp 7 tập 2a) Vì sao các góc B và C không thể là góc vuông hoặc góc tù? Cho tam giác ABC trong đó BC là cạnh lớn nhất. a) Vì sao các góc B và C không thể là góc vuông hoặc góc tù? b) Gọi AH là đường vuông góc kẻ từ A đến BC. So sánh AB + AC với BH + CH rồi chứng minh rằng AB + AC > BC. Giải
a) Giả sử \(\widehat B \ge 90^\circ\) => AC > BC (Trong một tam giác cạnh đối diện với góc vuông hoặc góc tù là cạnh lớn nhất) Trái giả thiết cạnh BC là cạnh lớn nhất Giả sử \(\widehat C \ge 90^\circ \) => AB > BC (Trong một tam giác cạnh đối diện với góc vuông hoặc góc tù là cạnh lớn nhất) Trái với giả thiết BC là cạnh lớn nhất Vậy \(\widehat B,\widehat C\) là các góc nhọn. b) Ta có điểm H nằm giữa B và C => BH + HC = BC (1) Ta có: AB > BH (đường xiên lớn hơn đường vuông góc) AC > CH (đường xiên lớn hơn đường vuông góc) Cộng từng vế ta có : AB + AC > BH + CH (2) Từ (1) và (2) suy ra: AB + AC > BC Sachbaitap.com
Xem lời giải SGK - Toán 7 - Xem ngay >> Học trực tuyến lớp 7 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 7 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
|
-
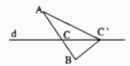
Câu 25 trang 41 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Nếu đặt ở C máy phát sóng truyền thanh có bán kính hoạt động bằng 40km thì thành phố B có nhận được tín hiệu không?
-
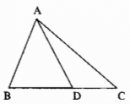
Câu 26 trang 41 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Chứng minh rằng AD nhỏ hơn nửa chu vi tam giác ABC.
-
Câu 27 trang 41 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Chứng minh rằng tổng MA + MB + MC lớn hơn nửa chu vi tam giác ABC.

 Tải ngay
Tải ngay