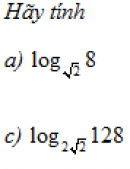Câu 2.22 trang 73 sách bài tập Giải tích 12 Nâng caoVới giá trị nào của a thì phương trình Với giá trị nào của a thì phương trình \({2^{ax^2 - 4x - 2a}} = {1 \over {{{\left( {\sqrt 2 } \right)}^{ - 4}}}}\) Có nghiệm duy nhất ? Giải \({1 \over {{{\left( {\sqrt 2 } \right)}^{ - 4}}}} = {\left( {\sqrt 2 } \right)^4} = {2^2}\) . Để phương trình đã cho có nghiệm duy nhất, điều kiện cần và đủ là phương trình \(a{x^2} - 4x - 2a = 2\) (1) Có nghiệm duy nhất +) Khi a = 0 thì phương trình có nghiệm duy nhất \(x = -{1 \over 2}\) +) Khi \(a \ne 0\) , (1) trở thành phương trình bậc hai \(a{x^2} - 4x - 2(a + 1) = 0\). Nó có nghiệm duy nhất khi và chỉ khi \(\Delta ' = 4 - 2(a + 1)a = 0\) Hay \({a^2} + a + 2 = 0\) . Điều này không xảy ra. Vậy phương trình đã cho có nghiệm duy nhất khi a = 0 Sachbaitap.com
Xem lời giải SGK - Toán 12 Nâng cao - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 2. Lũy thừa với số mũ thực
|
-

Câu 2.33 trang 76 sách bài tập Giải tích 12 Nâng cao
Trong các đẳng thức sau đây, đẳng thức nào đúng, đẳng thức nào sai ?
-
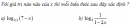
Câu 2.36 trang 76 sách bài tập Giải tích 12 Nâng cao
Với giá trị nào nào của x thì mỗi biểu thức sau đây xác định ?

 Tải ngay
Tải ngay