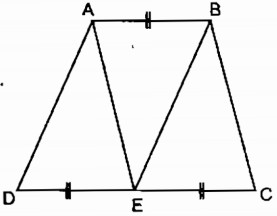
Câu 28 trang 90 Sách bài tập (SBT) Toán 8 tập 2Chứng minh rằng ba tam giác ADE, ABE và BEC đông dạng với nhau từng đôi một. Hình thang ABCD (AB // CD) có CD = 2AB. Gọi E là trung điểm của DC. Chứng minh rằng ba tam giác ADE, ABE và BEC đồng dạng với nhau từng đôi một. (Chú ý viết các đỉnh của hai tam giác đồng dạng theo thứ tự tương ứng với nhau).
Giải: Vì CD = 2AB (gt) nên AB \( = {1 \over 2}CD\) Vì E là trung điểm của CD nên DE = EC \( = {1 \over 2}CD\) Suy ra: AB = DE = EC Hình thang ABCD có đáy AB = EC nên hai cạnh bên AE và BC song song với nhau: Xét ∆ AEB và ∆ CBE, ta có: \(\widehat {ABE} = \widehat {BEC}\) (so le trong) \(\widehat {AEB} = \widehat {EBC}\) (so le trong) BE canh chung ⇒ ∆ AEB = ∆ CBE (g.c.g) (1) Hình thang ABED có đáy AB = DE nên hai cạnh bên AD và BE song song với nhau. Xét ∆ AEB và ∆ EAD, ta có: \(\widehat {BAE} = \widehat {AED}\) (so le trong) \(\widehat {AEB} = \widehat {EAD}\) (so le trong) AE cạnh chung ⇒ ∆ AEB = ∆ EAD (g.c.g) (2) Từ (1) và (2) suy ra: ∆ AEB = ∆ EAD = ∆ CBE. Do đó ba tam giác ADE, ABE và BEC đồng dạng với nhau từng đôi một. Sachbaitap.com
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 4. Khái niệm hai tam giác đồng dạng
|
-

Câu 29 trang 90 Sách bài tập (SBT) Toán 8 tập 2
Hai tam giác mà các cạnh có độ dài như sau có đồng dạng không ?
-

Câu 30 trang 90 Sách bài tập (SBT) Toán 8 tập 2
Hỏi rằng hai tam giác vuông ABC và A’B’C’ có đồng dạng với nhau không ? Vì sao ?
-
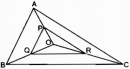
Câu 31 trang 90 Sách bài tập (SBT) Toán 8 tập 2
Chứng minh rằng tam giác PQR đồng dạng với tam giác ABC.

 Tải ngay
Tải ngay