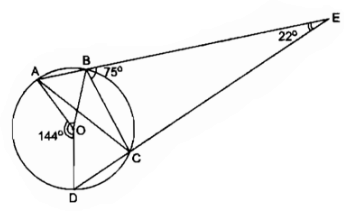
Câu 30 trang 105 Sách Bài Tập (SBT) Toán 9 Tập 2Chứng minh góc AOB = góc BAC. Hai dây cung AB và CD kéo dài cắt nhau tại điểm E ở ngoài đường tròn (O) (B nằm giữa A và E, C nằm giữa D và E). Cho biết \(\widehat {CDE}\) = 75 0, \(\widehat {CED} = {22^0}\), \(\widehat {AOD} = {144^0}\). Chứng minh \(\widehat {AOB} = \widehat {BAC}\). Giải
Trong đường tròn (O) ta có là góc có đỉnh ở ngoài đường tròn. \(\widehat E = {1 \over 2}\) (sđ \(\overparen{AD}\) - sđ \(\overparen{BC}\)) sđ \(\overparen{AD}\) = \(\widehat {AOD} = 144^\circ \) \( \Rightarrow \) 22º = \({{144^\circ - sđ \overparen{BC}} \over 2}\) Þ sđ \(\overparen{BC}\)= 144º - 2. 22º = 100º \(\widehat {BAC} = {1 \over 2}\) sđ \(\overparen{BC}\)(tính chất nội tiếp) \( \Rightarrow \) \(\widehat {BAC} = {1 \over 2}.100^\circ = 50^\circ \) Trong ∆ABC ta có \(\widehat {CBE}\) là góc ngoài tại đỉnh B. \( \Rightarrow \) \(\widehat {CBE} = \widehat {BAC} + \widehat {ACB}\) (tính chất góc ngoài của tam giác) \( \Rightarrow \) \(\widehat {ACB} = \widehat {CBE} - \widehat {BAC} = 75^\circ - 50^\circ = 25^\circ \) \(\widehat {ACB} = {1 \over 2}\widehat {AOB}\) (hệ quả góc nội tiếp) \(\widehat {AOB} = 2.\widehat {ACB} = 50^\circ \) Vậy \(\widehat {AOB} = \widehat {BAC} = 50^\circ \) Sachbaitap.com
Xem lời giải SGK - Toán 9 - Xem ngay >> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
|
-
Câu 33 trang 105 Sách Bài Tập (SBT) Toán 9 Tập 2
Tìm quỹ tích giao điểm của ba đường phân giác trong của tam giác đó.
-
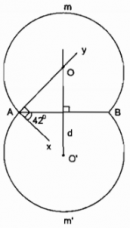
Câu 34 trang 105 Sách Bài Tập (SBT) Toán 9 Tập 2
Dựng cung chứa góc 42 độ trên đoạn thẳng AB = 3 cm.

 Tải ngay
Tải ngay