Tải ngay
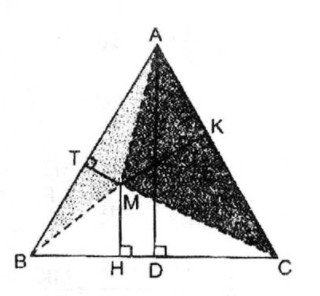
Câu 3.2 trang 161 Sách bài tập (SBT) Toán 8 tập 1Cho tam giác đều ABC và điểm M bất kì nằm trong tam giác đó. Đường thẳng đi qua điểm M và vuông góc với BC tại điểm H. Đường thẳng đi qua điểm M và vuông góc với CA tại điểm K. Đường thẳng đi qua điểm M và vuông góc với AB tại điểm T. Cho tam giác đều ABC và điểm M bất kì nằm trong tam giác đó. Đường thẳng đi qua điểm M và vuông góc với BC tại điểm H. Đường thẳng đi qua điểm M và vuông góc với CA tại điểm K. Đường thẳng đi qua điểm M và vuông góc với AB tại điểm T. Giải:
Giả sử ∆ ABC đều có cạnh bằng a, kẻ đường cao AD, đặt AD = h không đổi. Ta có: \(\eqalign{ & {S_{ABC}} = {1 \over 2}ah \cr & {S_{MAB}} = {1 \over 2}MT.a \cr & {S_{MAC}} = {1 \over 2}MK.a \cr & {S_{MBC}} = {1 \over 2}MH.a \cr & {S_{ABC}} = {S_{MAB}} + {S_{MAC}} + {S_{MBC}} \cr & {1 \over 2}a.h = {1 \over 2}MT.a + {1 \over 2}MK.a + {1 \over 2}MH.a \cr & = {1 \over 2}a.\left( {MT + MK + MH} \right) \cr} \) \( \Rightarrow MT + MK + MH = h\) không đổi Vậy tổng MT + MK + MH không phụ thuộc vào điểm M.
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.
Xem thêm tại đây:
Bài 3. Diện tích tam giác
|
-
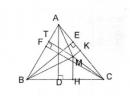
Câu 3.3 trang 161 Sách bài tập (SBT) Toán 8 tập 1
Cho hai tam giác ABC và DBC. Kẻ đường cao AH của tam giác ABC. Kẻ đường cao DK của tam giác DBC. Gọi S là diện tích của tam giác ABC. Gọi S’ là diện tích của tam giác DBC.
-
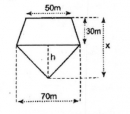
Câu 32 trang 161 Sách bài tập (SBT) Toán 8 tập 1-
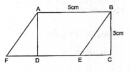
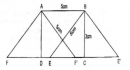
Tính x, biết đa giác ở hình 188 có diện tích là 3375 m2.
