Câu 3.7 trang 86 sách bài tập Đại số và Giải tích 11 Nâng caoCho số nguyên Cho số nguyên \(n \ge 2\) và cho số thực \({a_1},{a_2},...,{a_n}\) thuộc khoảng \(\left( {0;1} \right)\). Chứng minh rằng \(\left( {1 - {a_1}} \right)\left( {1 - {a_2}} \right)...\left( {1 - {a_n}} \right) > 1 - {a_1} - {a_2} - ... - {a_n}\) Giải Ta sẽ giải bài toán bằng phương pháp quy nạp Kí hiệu bất đẳng thức cần chứng minh theo yêu cầu của đề bài bởi (1) Với \(n = 2,\) xét hai số thực túy ý \({a_1},{a_2} \in \left( {0;1} \right)\) ta có \(\left( {1 - {a_1}} \right)\left( {1 - {a_2}} \right) \) \(= 1 - {a_1} - {a_2} + {a_1}{a_2} > 1 - {a_1} - {a_2}\) (do \({a_1},{a_2} > 0\) ) Như thế, (1) đúng khi \(n = 2\) Giả sử đã có (1) đúng khi \(n = k,k \in N^*\) và \(k \ge 2,\) Xét \(k + 1\) số thực tùy ý \({a_1},{a_2},...,{a_k},{a_{k + 1}}\) thuộc khoảng \(\left( {0;1} \right)\) Vì k số \({a_1},{a_2},...,{a_k}\) thuộc khoảng \(\left( {0;1} \right)\) nên theo giả thiết quy nạp ta có \(\left( {1 - {a_1}} \right)\left( {1 - {a_2}} \right)...\left( {1 - {a_k}} \right) > 1 - {a_1} - {a_2} - ... - {a_k}\) Từ đó, vì \(1 - {a_{k + 1}} > 0,\) suy ra \(\left( {1 - {a_1}} \right)\left( {1 - {a_2}} \right)...\left( {1 - {a_k}} \right)\left( {1 - {a_{k + 1}}} \right) >\) \(\left( {1 - {a_1} - {a_2} - ... - {a_k}} \right)\left( {1 - {a_{k + 1}}} \right)\) (2) Lại có \(\eqalign{ Từ (2) và (3) ta được \(\left( {1 - {a_1}} \right)\left( {1 - {a_2}} \right)...\left( {1 - {a_k}} \right)\left( {1 - {a_{k + 1}}} \right) > \) \(1 - {a_1} - {a_2} - ... - {a_k} - {a_{k + 1}}\) Như vậy (1) cũng đúng khi \(n = k + 1\) Từ các chứng minh trên suy ra có điều cần chứng minh theo yêu cầu của để bài. sachbaitap.com
Xem lời giải SGK - Toán 11 Nâng cao - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Bài 1: Phương pháp quy nạp toán học
|
-
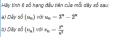
Câu 3.8 trang 86 sách bài tập Đại số và Giải tích 11 Nâng cao
Hãy tính 6 số hạng đầu tiên của mỗi dãy số sau:

 Tải ngay
Tải ngay










