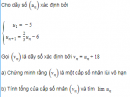Câu 4.11 trang 135 sách bài tập Đại số và Giải tích 11 Nâng caoCho dãy số xác định bởi Cho dãy số \(\left( {{u_n}} \right)\) xác định bởi \(\left\{ \matrix{ Chứng minh rằng: a) \({u_n} > 1\) với mọi n b) \({u_{n + 1}} - 1 < {{{u_n} - 1} \over 2}\) với mọi n c) Tìm \(\lim {u_n}\) Giải a) Chứng minh bằng phương pháp quy nạp b) \({u_{n + 1}} - 1 < \sqrt {{u_n}} - 1 = {{{u_n} - 1} \over {\sqrt {{u_n}} + 1}} \le {{{u_n} - 1} \over 2}\) với mọi n vì \(\sqrt {{u_n}} > 1\) c) Đặt \({v_n} = {u_n} - 1,\) ta có \(0 < {v_{n + 1}} \le {1 \over 2}{v_n}\) với mọi n Do đó \({v_2} \le {1 \over 2}{v_1}\); \({v_3} \le {1 \over 2}{v_2} \le {\left( {{1 \over 2}} \right)^2}{v_1}\) Bằng phương pháp quy nạp ta chứng minh được \(0 < {v_n} \le {\left( {{1 \over 2}} \right)^{n - 1}}{v_1} = 9{\left( {{1 \over 2}} \right)^{n - 1}}\) Vì \(\lim {\left( {{1 \over 2}} \right)^{n - 1}} = 0\) nên từ đó suy ra \(\lim {v_n} = 0\) Vậy \({{\mathop{\rm limu}\nolimits} _n} = 1\) Sachbaitap.com
Xem lời giải SGK - Toán 11 Nâng cao - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Bài 2: Dãy có giới hạn hữu hạn
|
-

Câu 4.13 trang 135 sách bài tập Đại số và Giải tích 11 Nâng cao
Người ta xếp các hình vuông kề với nhau như trong hình 4.1 dưới đây, mỗi hình vuông có độ dài cạnh bằng nửa độ dài cạnh của hình vuông trước nó.
-

Câu 4.14 trang 136 sách bài tập Đại số và Giải tích 11 Nâng cao
Một quả bóng cao su được thả từ độ cao 81m. Mỗi lần chạm đất, quả bóng lại nảy lên hai phần ba độ cao của lần rơi trước.
-

Câu 4.15 trang 136 sách bài tập Đại số và Giải tích 11 Nâng cao
Biểu diễn các số thập phân vô hạn tuần hoàn sau đây dưới dạng phân số:

 Tải ngay
Tải ngay