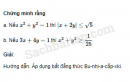Câu 4.20 trang 105 SBT Đại số 10 Nâng caoGiải bài tập Câu 4.20 trang 105 SBT Đại số 10 Nâng cao. Tìm giá trị nhỏ nhất của các hàm số sau a. \(f\left( {\rm{x}} \right) = {x^2} + \dfrac{{16}}{{{x^2}}}\) b. \(g\left( {\rm{x}} \right) = \dfrac{1}{x} + \dfrac{2}{{1 - x}}\) với \(0 < x < 1.\) Giải: a. \({x^2} + \dfrac{{16}}{{{x^2}}} \ge 2\sqrt {{{x}^2}.\dfrac{{16}}{{{x^2}}}} = 8.\) Đẳng thức xảy ra khi \(x = ±2.\)- Vậy giá trị nhỏ nhất của \(f(x)\) là 8 khi \(x = ±2.\) b. Do \(0 < x < 1\) nên \(1 – x > 0.\) Ta có \(\eqalign{& {1 \over x} = {{1 - x} \over x} + 1; \cr& {2 \over {1 - x}} = {{2x} \over {1 - x}} + 2; \cr & {1 \over x} + {2 \over {1 - x}} \cr & = {{1 - x} \over x} + {{2x} \over {1 - x}} + 3 \ge 2\sqrt {{{1 - x} \over x}.{{2x} \over {1 - x}}} + 3 \cr & = 2\sqrt 2 + 3 \cr} \) Đẳng thức xảy ra khi \(\dfrac{{1 - x}}{x} = \dfrac{{2x}}{{1 - x}}\) và \(0 < x < 1\) tức là \(x = - 1 + \sqrt 2 .\) Vậy giá trị nhỏ nhất của \(g(x)\) là \(2\sqrt 2 + 3\) khi \(x = - 1 + \sqrt 2 \) Sachbaitap.com
Xem thêm tại đây:
Bài 1. Bất đẳng thức và chứng minh bất đẳng thức
|

 Tải ngay
Tải ngay