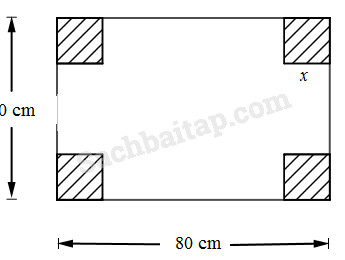
Câu 4.22 trang 105 SBT Đại số 10 Nâng cao

Cho một tấm tôn hình chữ nhật có kích thước 80 cm x 50 cm. Hãy cắt đi ở bốn góc vuông những hình vuông bằng nhau để khi gập lại theo mép cắt thì được một cái hộp (không nắp) có thể tích lớn nhất.

Giải:

Gọi cạnh hình vuông được cắt là \(9x\) (\(0 < x < 25\), đơn vị : xentimét)

Thể tích V của cái hộp là

\(V = x\left( {80 - 2{x}} \right)\left( {50 - 2{x}} \right)\)

Khi đó ta có

\(\begin{array}{l}12V = 6{x}\left( {80 - 2{x}} \right)\left( {100 - 4{x}} \right)\\ \le {\left( {\dfrac{{6{x} + 80 - 2{x} + 100 - 4{x}}}{3}} \right)^3} = {60^{3.}}\end{array}\)

Suy ra \(V \le \dfrac{{{{60}^3}}}{{12}}\) hay \(V \le 18\,000\)

Đẳng thức xảy ra khi và chỉ khi \(6x = 80 – 2x = 100 – 4x\) tức là \(x = 10.\)

Giá trị lớn nhất của V là 18000 cm³ khi \(x = 10 (cm)\)

Vậy phải cắt đi ở bốn góc vuông của hình chữ nhật ban đầu những hình vuông có cạnh 10 cm.

Nhận xét. Nếu xét \(4V = 4{x}\left( {80 - 2{x}} \right)\left( {50 - 2{x}} \right)\) thì 4V là tích của ba thừa số có tổng không đổi (bằng 130), ta vẫn có bất đẳng thức \(4V \le {\left( {\dfrac{{130}}{3}} \right)^3}\) nhưng đẳng thức không thể xảy ra và không có giá trị nào của x thỏa mãn

\(80 - 2{x} = 50 - 2{x}\)

Sachbaitap.com