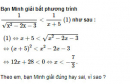Câu 4.32 trang 107 SBT Đại số 10 Nâng cao

Để giải bất phương trình $\sqrt {{x} - 2}  > \sqrt {2{x} - 3} \,\left( 1 \right),$ bạn Nam đã làm như sau:

Do hai vế của bất phương trình (1) luôn không âm nên (1) tương đương với ${\left( {\sqrt {{x} - 2} } \right)^2} > {\left( {\sqrt {2{x} - 3} } \right)^2}$ hay $x - 2 > 2{x} - 3.$ Do đó $x < 1$.

Vậy tập nghiệm của (1) là $\left( { - \infty ,1} \right)$

Theo em, bạn Nam giải đã đúng chưa, vì sao ?

Giải:

Sai lầm của bạn Nam là không để ý đến điều kiện xác định của phương trình $D = \left[ {2; + \infty } \right).$ Hai vế của (1) chỉ không âm khi $x ∈ D$ chứ không phải với mọi $x ∈ R$. Vì vậy, khi tìm ra $x < 1$ cần phải đối chiếu với điều kiện $x \in \left[ {2; + \infty } \right)$ để kết luận bất phương trình (1) vô nghiệm.

Sachbaitap.com