Tải ngay
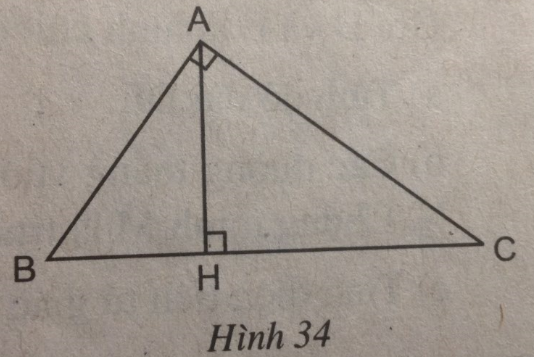
Câu 48 trang 95 Sách bài tập (SBT) Toán 8 tập 2Chứng minh rằng Cho tam giác ABC (\(\widehat A = 90^\circ \)) có đường cao AH (h.34) Chứng minh rằng \(A{H^2} = BH.CH\) Giải: (hình 34 trang 95 sbt)
Xét hai tam giác vuông HBA và HAC, ta có: \(\widehat {BHA} = \widehat {AHC} = 90^\circ \) \(\widehat B = \widehat {HAC}\) (hai góc cùng phụ góc C) Suy ra: ∆ HBA đồng dạng ∆ HAC (g.g) Suy ra: \({{HA} \over {HB}} = {{HC} \over {HA}}\) Vậy \(A{H^2} = HB.HC\) Sachbaitap.com
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.
Xem thêm tại đây:
Bài 8. Các trường hợp đồng dạng của tam giác vuông
|
-
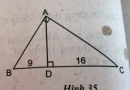
Câu 49 trang 96 Sách bài tập (SBT) Toán 8 tập 2
Đường cao của một tam giác vuông xuất phát từ đỉnh góc vuông chia cạnh huyền thành hai đoạn thẳng có độ dài là 9cm và 16cm. Tính độ dài các cạnh của tam giác vuông đó (h.35)
-
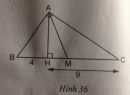
Câu 50 trang 96 Sách bài tập (SBT) Toán 8 tập 2
Tính diện tích tam giác AMH, biết rằng BH = 4cm, CH = 9cm.
-
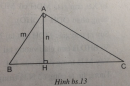
Câu 8.2 trang 96 Sách bài tập (SBT) Toán 8 tập 2
Hãy tính độ dài các cạnh còn lại của tam giác (chính xác đến hai chữ số thập phân)
