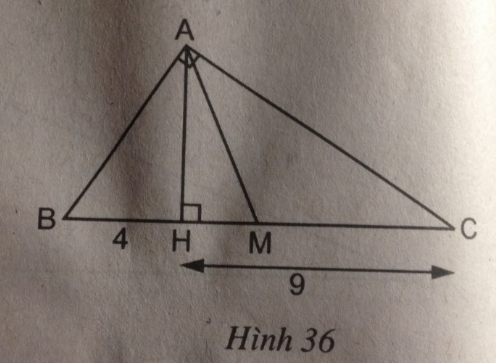
Câu 50 trang 96 Sách bài tập (SBT) Toán 8 tập 2Tính diện tích tam giác AMH, biết rằng BH = 4cm, CH = 9cm. Tam giác vuông ABC (\(\widehat A = 90^\circ \)) có đường cao AH và trung tuyến AM (h.36). Tính diện tích tam giác AMH, biết rằng BH = 4cm, CH = 9cm. Giải: Xét hai tam giác vuông HBA và HAC, ta có: \(\widehat {BHA} = \widehat {AHC} = 90^\circ \) \(\widehat C = \widehat {HAC}\) (hai góc cùng phụ góc B) Suy ra: ∆ HBA đồng dạng ∆ HAC (g.g) Suy ra: \({{HA} \over {HB}} = {{HC} \over {HA}}\) \( \Rightarrow H{A^2} = HB.HC = 4.9 = 36\) (cm) Suy ra: AH = 6(cm) Lại có: \(BM = {1 \over 2}BC = {1 \over 2}.\left( {9 + 4} \right) = {1 \over 2}.13 = 6,5\) (cm) Mà \(HM = BM - BH = 6,5 - 4 = 2,5\) (cm) Vậy \({S_{AHM}} = {1 \over 2}AH.HM = {1 \over 2}.6.2,5 = 7,5(c{m^2})\) Sachbaitap.com
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 8. Các trường hợp đồng dạng của tam giác vuông
|
-
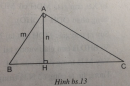
Câu 8.2 trang 96 Sách bài tập (SBT) Toán 8 tập 2
Hãy tính độ dài các cạnh còn lại của tam giác (chính xác đến hai chữ số thập phân)
-
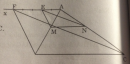
Câu 51 trang 97 Sách bài tập (SBT) Toán 8 tập 2
Vẽ đoạn thẳng MN. Hỏi rằng hai đường thẳng MN và BC có song song với nhau không ? Vì sao ?

 Tải ngay
Tải ngay