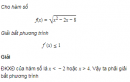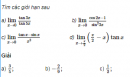Câu 5.14 trang 181 sách bài tập Đại số và Giải tích 11 Nâng caoCho hàm số. Tìm m để Cho hàm số \(f\left( x \right) = {{m{x^3}} \over 3} - {{m{x^2}} \over 2} + \left( {3 - m} \right)x - 2\) Tìm m để a) \(f'\left( x \right)\) với mọi x; b) \(f'\left( x \right)\) có hai nghiệm phân biệt cùng dấu; c) Chứng minh rằng trong trường hợp có hai nghiệm(hai nghiệm có thể trùng nhau) thì các nghiệm thỏa mãn một hệ thức độc lập với m. Giải Với mọi \(x \in R,\) ta có \(f'\left( x \right) = m{x^2} - mx + 3 - m.\) a) Ta phải xét hai trường hợp sau đây 1. Với \(m = 0\) thì \(f'\left( x \right) = 3 > 0\,\,\,\left( {\forall x \in R} \right).\) Vậy \(m = 0\) là một giá trị cần tìm. 2. Với \(m \ne 0\) (khi đó \(f'(x)\) là một tam thức bậc hai) thì ta phải tìm \(m\) sao cho \(\left\{ \matrix{m > 0 \hfill \cr\Delta = {m^2} - 4\left( {3 - m} \right) = m\left( {5m - 12} \right) < 0 \hfill \cr} \right.\) \(\Leftrightarrow 0 < m < {{12} \over 5}\) Vậy các giá trị của \(m\) thỏa mãn điều kiên của bài toán là \(0 \le m < {{12} \over 5}.\) Chú ý. Không được phép hai trường hợp 1 và 2 (vì trong trường hợp 1, \(f\left( x \right)\) không phải là một tam thức bậc hai nên không áp đụngk được định lí về dấu của tam thức bậc hai). b) Để \(f'(x)\) có hai nghiệm phân biệt cùng dấu thì phải tìm \(m\) sao cho tam thức bậc haicó hai nghiệm phân biệt và tích của chúng là \(P = {c \over a} > 0\) (hay số 0 nằm ngoài hai nghiệm) tức là \(\left\{ \matrix{m \ne 0 \hfill \cr\Delta = m\left( {5m - 12} \right) > 0 \hfill \cr{{3 - m} \over m} > 0\,\,\,\left( {hay\,\,m\left( {3 - m} \right) > 0} \right) \hfill \cr} \right.\) \(\Leftrightarrow {{12} \over 5} < m < 3.\) c) Vì có hai nghiệm (hai nghiệm có thể trùng nhau) nên ta có \(\left\{ \matrix{m \ne 0 \hfill \cr\Delta \ge 0 \hfill \cr{x_1} + {x_2} = {m \over m} = 1 \hfill \cr{x_1}{x_2} = {{3 - m} \over m} \hfill \cr} \right.\,\, \Leftrightarrow \left\{ \matrix{m < 0\text{ hoặc }m \ge {2 \over 5} \hfill \cr{x_1} + {x_2} = 1. \hfill \cr} \right.\) Vậy hệ thức phải tìm là \({x_1} + {x_2} = 1.\) Sachbaitap.com
Xem lời giải SGK - Toán 11 Nâng cao - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Bài 2: Các quy tắc tính đạo hàm
|
-
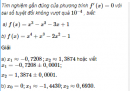
Câu 5.15 trang 181 sách bài tập Đại số và Giải tích 11 Nâng cao
Tìm nghiệm gần đúng của phương trình
-
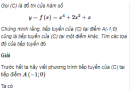
Câu 5.18 trang 181 sách bài tập Đại số và Giải tích 11 Nâng cao
Gọi (C) là đồ thị của hàm số. Chứng minh rằng, tiếp tuyến của (C) tại điểm A(-1;0) cũng là tiếp tuyến của (C) tại một điểm khác. Tìm các tọa độ của tiếp tuyến đó.

 Tải ngay
Tải ngay