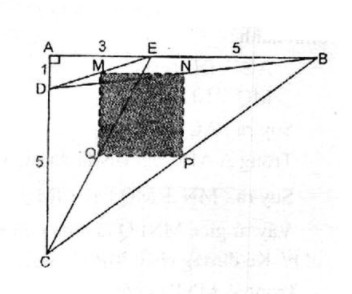
Câu 5.3 trang 163 Sách bài tập (SBT) Toán 8 tập 1Tính diện tích của tứ giác MNPQ. Cho tam giác vuông ABC, có hai cạnh góc vuông là AC = 6cm và AB = 8cm. Trên cạnh AC lấy điểm D sao cho CD = 5cm. Trên cạnh AB lấy điểm E sao cho EB = 5cm. Gọi M, N, P, Q tương ứng là trung điểm của các đoạn thẳng DE, DB, BC và CE. Tính diện tích của tứ giác MNPQ. Giải:
Trong ∆ EDC ta có: M là trung điểm của ED Q là trung điểm của EC nên MQ là đường trung bình của ∆ EDC ⇒ MQ = \({1 \over 2}\)CD = 2,5 (cm) và MQ // CD Trong ∆ BDC ta có: N là trung điểm của BD P là trung điểm của BC nên NP là đường trung bình của ∆ BDC ⇒ NP = \({1 \over 2}\)CD = 2,5 (cm) Trong ∆ DEB ta có: M là trung điểm của DE N là trung điểm của DB nên MN là đường trung bình của ∆ DEB ⇒ MN = \({1 \over 2}\)BE = 2,5 (cm) và MN // BE Trong ∆ CEB ta có: Q là trung điểm của CE P là trung điểm của CB nên QP là đường trung bình của ∆ CEB ⇒ QP = \({1 \over 2}\)BE = 2,5 (cm) Suy ra: MN = NP = PQ = QM (1) MQ // CD hay MQ // AC AC ⊥ AB (gt) ⇒ MQ ⊥ AB MN // BE hay MN // AB Suy ra: MQ ⊥ MN hay \(\widehat {QMN} = 90^\circ \) (2) Từ (1) và (2) suy ra tứ giác MNPQ là hình vuông \({S_{MNPQ}} = M{N^2} = {\left( {2,5} \right)^2} = 6,25(c{m^2})\)
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 5. Diện tích hình thoi
|
-
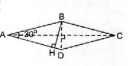
Câu 43 trang 163 Sách bài tập (SBT) Toán 8 tập 1
Tính diện tích hình thoi, biết cạnh của nó dài 6,2cm và một trong các góc của nó có số đo bằng 30°
-
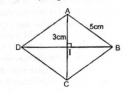
Câu 44 trang 163 Sách bài tập (SBT) Toán 8 tập 1
Cho hình thoi ABCD, biết AB = 5cm, AI = 3cm (I là giao điểm của hai đường chéo). Hãy tính diện tích hình thoi đó.
-
Câu 45 trang 163 Sách bài tập (SBT) Toán 8 tập 1
Hãy vẽ một tứ giác có hai đường chéo vuông góc với nhau, biết độ dài hai đường chéo đó là a và a. Hỏi có thể vẽ được bao nhiêu hình như vậy ?
-
Câu 46 trang 163 Sách bài tập (SBT) Toán 8 tập 1
Hai đường chéo của một hình thoi có độ dài là 16cm và 12cm. Tính: a. Diện tích hình thoi b. Độ dài cạnh hình thoi c. Độ dài đường cao hình thoi

 Tải ngay
Tải ngay