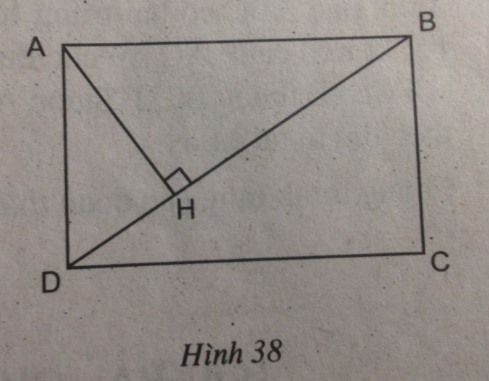
Câu 53 trang 97 Sách bài tập (SBT) Toán 8 tập 2Chứng minh ∆ AHB đồng dạng ∆ BCD; Cho hình chữ nhật ABCD có AB = a = 12 cm, BC = b = 9cm. Gọi H là chân đường vuông góc kẻ từ A xuống BD (h.38) a. Chứng minh ∆ AHB đồng dạng ∆ BCD; b. Tính độ dài đoạn thẳng AH; c. Tính diện tích tam giác AHB. Giải:
Xét ∆ AHB và ∆ BCD, ta có: \(\widehat {AHB} = \widehat {BCD} = 90^\circ \) AB // CD (gt) \(\widehat {ABH} = \widehat {BDC}\) (so le trong) Vậy ∆ AHB đồng dạng ∆ BCD (g.g) b. Vì ∆ AHB đồng dạng ∆ BCD nên: \({{AH} \over {BC}} = {{AB} \over {BD}}\) Suy ra: \(AH = {{AB.BC} \over {BD}}\) Áp dụng định lí Pi-ta-go vào tam giác vuông BCD, ta có: \(\eqalign{ & B{D^2} = B{C^2} + C{D^2} = B{C^2} + A{B^2} \cr & = {12^2} + {9^2} = 225 \cr} \) Suy ra: BD = 15 (cm) Vậy \(AH = {{12.9} \over {15}} = 7,2\) (cm). c. Vì ∆ AHB đồng dạng ∆ BCD nên k = \({{AH} \over {BC}} = {{7,2} \over 9} = 0,8\) Ta có: \({{{S_{AHB}}} \over {{S_{BCD}}}} = {k^2} = {\left( {0,8} \right)^2} = 0,64\) \(\Rightarrow {S_{AHB}} = 0,64{S_{BCD}}\) \({S_{BCD}} = {1 \over 2}BC.CD = {1 \over 2}.12.9 = 54(c{m^2})\) Vậy \({S_{AHB}} = 0,64.{S_{BCD}} = 0,64.54 = 34,56(c{m^2})\) Sachbaitap.com
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Ôn tập chương III - Tam giác đồng dạng
|
-
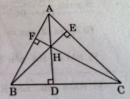
Câu 55 trang 98 Sách bài tập (SBT) Toán 8 tập 2
Tam giác ABC có ba đường cao AD, BE, CF đồng quy tại H. Chứng minh rằng AH.DH = BH.EH = CH.FH
-
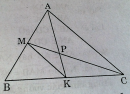
Câu 56 trang 98 Sách bài tập (SBT) Toán 8 tập 2
Chứng minh rằng AK và CM là các trung tuyến của tam giác ABC.
-
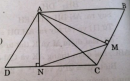
Câu 57 trang 98 Sách bài tập (SBT) Toán 8 tập 2
Chứng minh rằng tam giác MAN đồng dạng với tam giác ABC.

 Tải ngay
Tải ngay