Tải ngay
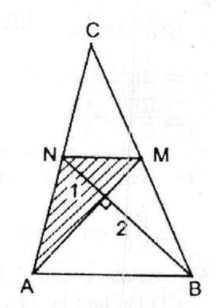
Câu 54 trang 166 Sách bài tập (SBT) Toán 8 tập 1Tam giác ABC có hai trung tuyến AM và BN vuông góc với nhau. Hãy tính diện tích tam giác đó theo AM và BN Tam giác ABC có hai trung tuyến AM và BN vuông góc với nhau. Hãy tính diện tích tam giác đó theo AM và BN Giải:
Tứ giác ABMN có hai đường chéo vuông góc. \({S_{ABMN}} = {1 \over 2}AM.BN\) ∆ ABM và ∆ AMC có chung chiều cao kẻ từ A cạnh đáy BM = MC \( \Rightarrow {S_{ABM}} = {S_{AMC}} = {1 \over 2}{S_{ABC}}\) ∆ MAN và ∆ MNC có chung chiều cao kẻ từ M, cạnh đáy AN = NC \(\eqalign{ & \Rightarrow {S_{MAN}} = {S_{MNC}} = {1 \over 2}{S_{AMC}} = {1 \over 4}{S_{ABC}} \cr & {S_{ABMN}} = {S_{ABM}} + {S_{MNA}} = {1 \over 2}{S_{ABC}} + {1 \over 4}{S_{ABC}} = {3 \over 4}{S_{ABC}} \cr & \Rightarrow {S_{ABC}} = {4 \over 3}{S_{ABMN}} = {4 \over 3}.{1 \over 2}.AM.BN = {2 \over 3}AM.BN \cr} \)
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.
Xem thêm tại đây:
Ôn tập chương II - Đa giác - Diện tích đa giác
|
-
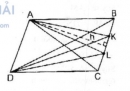
Câu 55 trang 166 Sách bài tập (SBT) Toán 8 tập 1
Cho hình bình hành ABCD. Gọi K và L là hai điểm thuộc cạnh BC sao cho BK = KL = LC. Tính tỉ số diện tích của : a. Các tam giác DAC và DCK b. Tam giác DAC và tứ giác ADLB c. Các tứ giác ABKD và ABLD
-
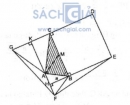
Câu 56 trang 166 Sách bài tập (SBT) Toán 8 tập 1
Cho tam giác ABC vuông ở A và có BC = 2 AB = 2a. Ở phía ngoài tam giác, ta vẽ hình vuông BCDE, tam giác đều ABF và tam giác đều ACG.
