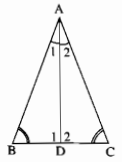
Câu 55 trang 145 Sách Bài Tập (SBT) Toán lớp 7 tập 1Chứng minh rằng DB = DC, AB = AC. Cho tam giác ABC có \(\widehat B = \widehat C\). Tia phân giác góc A cắt BC tại D. Chứng minh rằng DB = DC, AB = AC. Giải
Trong ∆ADB, ta có: \(\widehat B + \widehat {{A_1}} + \widehat {{D_1}} = 180^\circ \) (tổng ba góc trong tam giác) Suy ra: \(\widehat {{D_1}} = 180^\circ - \left( {\widehat B + \widehat {{A_1}}} \right)\) (1) Trong ∆ADC, ta có: \(\widehat C + \widehat {{D_2}} + \widehat {{A_2}} = 180^\circ \) (tổng ba góc trong tam giác) Suy ra: \(\widehat {{D_2}} = 180^\circ - \left( {\widehat C + \widehat {{A_2}}} \right)\) (2) \(\widehat B = \widehat C\left( {gt} \right)\); \(\widehat {{A_1}} = \widehat {{A_2}}\left( {gt} \right)\) (3) Từ (1), (2) và (3) suy ra: \(\widehat {{D_1}} = \widehat {{D_2}}\) Xét ∆ADB và ∆ADC, ta có: \(\widehat {{A_1}} = \widehat {{A_2}}\) AD cạnh chung \(\widehat {{D_1}} = \widehat {{D_2}}\) (chứng minh trên) Suy ra: ∆ADB = ∆ADC(g.c.g) Vậy: AB = AC (2 cạnh tương ứng) DB = DC (2 cạnh tương ứng) Sachbaitap.com
Xem lời giải SGK - Toán 7 - Xem ngay >> Học trực tuyến lớp 7 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 7 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
|
-
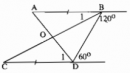
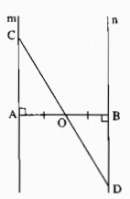
Câu 56 trang 145 Sách Bài Tập (SBT) Toán lớp 7 tập 1
Chứng minh rằng O là trung điểm của mỗi đoạn thẳng AD, BC.

 Tải ngay
Tải ngay