Tải ngay
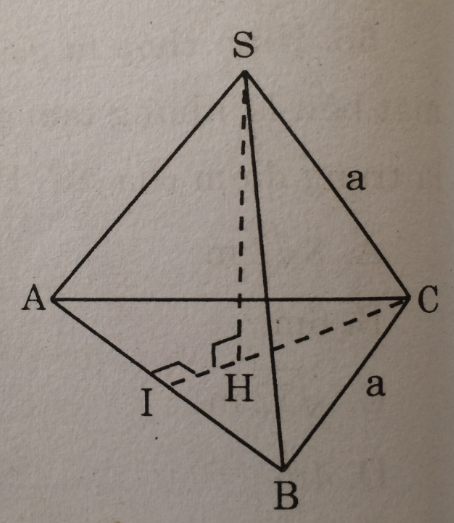
Câu 58 trang 149 Sách bài tập (SBT) Toán 8 tập 2Tính diện tích toàn phần của hình chóp tam giác đều theo các kích thước cho ở hình 145. Tính diện tích toàn phần của hình chóp tam giác đều theo các kích thước cho ở hình 145. (xem hình 145)
Giải: Hình vẽ đã cho là hình chóp có ba mặt xung quanh và mặt đáy là các tam giác đều bằng nhau có cạnh là a. Áp dụng định lí Pi-ta-go vào tam giác vuông CIA, ta có: Suy ra: \(C{I^2} = A{C^2} - A{I^2} = {a^2} - {\left( {{a \over 2}} \right)^2} = {{3{a^2}} \over 4}\) Vậy CI = \({{a\sqrt 3 } \over 2}\) Ta có: \({S_{ABC}} = {1 \over 2}.a.{{a\sqrt 3 } \over 2} = {{{a^2}\sqrt 3 } \over 4}\) (đvdt) Vậy diện tích toàn phần của hình chóp tam giác đều là: \({S_{TP}} = 4.{{{a^2}\sqrt 3 } \over 4} = {a^2}\sqrt 3 \) (đvdt) Sachbaitap.com
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.
Xem thêm tại đây:
Bài 8. Diện tích xung quanh của hình chóp đều
|
-
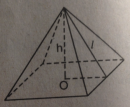
Câu 59 trang 150 Sách bài tập (SBT) Toán 8 tập 2
Cho hình chóp tứ giác đều (h.146). Xem hình và điền số thích hợp vào các ô còn trống ở bảng sau:
-
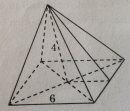
Câu 60 trang 150 Sách bài tập (SBT) Toán 8 tập 2
Một hình chóp tứ giác đều có độ dài cạnh đáy là 6cm, chiều cao là 4cm thì diện tích xung quanh là:
-
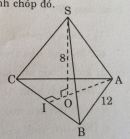
Câu 61 trang 150 Sách bài tập (SBT) Toán 8 tập 2
Hình chóp đều S.ABC có cạnh đáy a = 12cm, chiều cao h = 8cm. Hãy tính diện tích xung quanh của hình chóp đó.
-
Câu 62 trang 150 Sách bài tập (SBT) Toán 8 tập 2
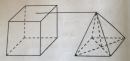
Một hình chóp tứ giác đều và một lăng trụ đứng tứ giác đều như hình 147 dưới đây (cạnh đáy và chiều cao bằng nhau):
