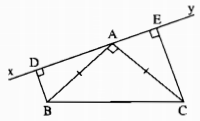
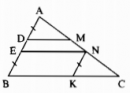
Câu 61 trang 145 Sách Bài Tập (SBT) Toán lớp 7 tập 1

Cho tam giác ABC vuông tại A có AB = AC. Qua A kẻ đường thẳng xy (B, C nằm cùng phía đối với xy). Kẻ BD và CE vuông góc với xy. Chứng minh rằng:

a) ∆BAD = ∆ACE

b) DE = BD + CE

Giải

a) Ta có: $\widehat {BA{\rm{D}}} + \widehat {BAC} + \widehat {CA{\rm{E}}} = 180^\circ$ (kề bù)

Mà $\widehat {BAC} = 90^\circ \left( {gt} \right) \Rightarrow \widehat {BA{\rm{D}}} + \widehat {CA{\rm{E}}} = 90^\circ$            (1)

Trong ∆AEC, ta có:

$\widehat {A{\rm{E}}C} = 90^\circ  \Rightarrow \widehat {CA{\rm{E}}} + \widehat {AC{\rm{E}}}{\rm{ = 90}}^\circ$                   (2)

Từ (1) và (2) suy ra: $\widehat {BA{\rm{D}}} = \widehat {AC{\rm{E}}}$

Xét hai tam giác vuông AEC và BDA, ta có: 

$\widehat {A{\rm{E}}C} = \widehat {B{\rm{D}}A} = 90^\circ$

AC = AB (gt)

$\widehat {AC{\rm{E}}} = \widehat {BA{\rm{D}}}$ (chứng minh trên)

Suy ra:  ∆AEC = ∆BDA (cạnh huyền, góc nhọn)

b) Ta có: ∆AEC = ∆BDA

=> AE = BD và EC = DA

Mà DE = DA + AE

Vậy: DE = CE + BD 

Sachbaitap.com