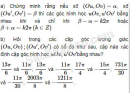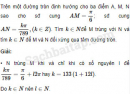Câu 6.14 trang 197 SBT Đại số 10 Nâng cao

a) Trong các góc lượng giác có tia đầu \(Ou\), tia cuối \(Ov\) cho trước, chứng minh rằng, có một góc lượng giác duy nhất \(\left( {Ou,Ov} \right)\)có số đo \(\alpha , - \pi  < \alpha  \le \pi \) và chứng minh rằng \(\left| \alpha  \right|\) là số đo rađian của góc hình học \(uOv\).

b) Tìm số đo của góc hình học \(uOv\), biết góc lượng giác \(\left( {Ou,Ov} \right)\) có số đo là:

• \(\dfrac{{9\pi }}{7};\dfrac{{ - 5\pi }}{8};\dfrac{{106\pi }}{9}; - 2003\)

• \({220^0}; - {235^0};{1945^0}; - {2003^0}.\)

Giải:

a) Nếu một góc lượng giác \(\left( {Ou,Ov} \right)\) có số đo \(\alpha , - \pi  < \alpha  \le \pi \), thì mọi góc lượng giác \(\left( {Ou,Ov} \right)\) khác có số đo \(\alpha  + k2\pi \left( {k \in Z\backslash \left\{ 0 \right\}} \right)\), nhưng dễ thấy \(\alpha  + k2\pi  \notin \left( { - \pi ;\pi } \right]\), với k nguyên khác 0, vậy góc lượng giác đó là duy nhất.

Khi hai tia \(Ou,Ov\) đối nhau thì một góc lượng giác \(\left( {Ou,Ov} \right)\) có số đo là \(\pi \) và \(\pi \) cũng là số đo rađian của góc bẹt uOv. Khi Ou, Ov không đối nhau thì số đo góc hình học uOv là \(\beta \), \(0 \le \beta  < \pi \) và sđ\(\left( {Ou,Ov} \right)\) là \(\beta  + k2\pi \) hoặc \( - \beta  + k2\pi \left( {k \in Z} \right)\) tức là:

sđ \(\left( {Ou,Ov} \right) = \alpha  + k2\pi ;\left| \alpha  \right| = \beta \).

b) Số đo góc hình học uOv cần tìm theo thứ tự là

• \(\dfrac{{5\pi }}{7};\dfrac{{5\pi }}{8};\dfrac{{2\pi }}{9}; \approx 1,336\) (do \(2003 \approx 319.2\pi  - 1,336\) và \( - \pi  <  - 1,336 \le \pi \));

• \({140^0};{125^{0;}}{145^0};{157^0}.\)

Sachbaitap.com