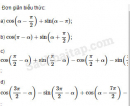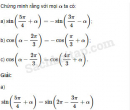Câu 6.29 trang 200 SBT Đại số 10 Nâng caoGiải bài tập Câu 6.29 trang 200 SBT Đại số 10 Nâng cao Cho \(\tan \alpha + \cot \alpha = m\), hãy tính theo \(m\) a) \({\tan ^2}\alpha + {\cot ^2}\alpha ;\) b) \(\left| {\tan \alpha - \cot \alpha } \right|;\) c) \({\tan ^3}\alpha + {\cot ^3}\alpha .\) Giải: Cho \(\tan \alpha + \cot \alpha = m\), ta có: a) \(\begin{array}{l}{\tan ^2}\alpha + {\cot ^2}\alpha \\ = {\left( {{{\tan }^2}\alpha + \cot \alpha } \right)^2} - 2\tan \alpha \cot \alpha \\ = {m^2} - 2\end{array}\) b) \(\begin{array}{l}{\left( {\tan \alpha - \cot \alpha } \right)^2}\\ = {\tan ^2}\alpha + {\cot ^2}\alpha - 2\tan \alpha \cot \alpha \\ = {m^2} - 4\end{array}\) Vậy \(\left| {\tan \alpha - \cot \alpha } \right| = \sqrt {{m^2} - 4} \) (để ý rằng, do \(\tan \alpha .\cot \alpha = 1\) nên \(\left| {\tan \alpha + \cot \alpha } \right| \ge 2\), từ đó \({m^2} \ge 4\)) c) \(\begin{array}{l}{\tan ^3}\alpha + {\cot ^3}\alpha \\ = {\left( {\tan \alpha + \cot \alpha } \right)^3} - 3\tan \alpha \cot \alpha \left( {\tan \alpha + \cot \alpha } \right)\\ = {m^3} - 3m\end{array}\) Sachbaitap.com
|

 Tải ngay
Tải ngay