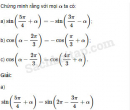Câu 6.32 trang 200 SBT Đại số 10 Nâng caoGiải bài tập Câu 6.32 trang 200 SBT Đại số 10 Nâng cao Đơn giản biểu thức: a) \(\cos \left( {\alpha - \dfrac{\pi }{2}} \right) + \sin \left( {\alpha - \pi } \right);\) b) \(\cos \left( {\pi - \alpha } \right) + \sin \left( {\alpha + \dfrac{\pi }{2}} \right);\) c) \(\cos \left( {\dfrac{\pi }{2} - \alpha } \right) + \sin \left( {\dfrac{\pi }{2} - \alpha } \right) - \cos \left( {\dfrac{\pi }{2} + \alpha } \right) - \sin \left( {\dfrac{\pi }{2} + \alpha } \right)\); d) \(\cos \left( {\dfrac{{3\pi }}{2} - \alpha } \right) - \sin \left( {\dfrac{{3\pi }}{2} - \alpha } \right) + \cos \left( {\alpha - \dfrac{{7\pi }}{2}} \right) - \sin \left( {\alpha - \dfrac{{7\pi }}{2}} \right)\); e) \(\cos \left( {\dfrac{\pi }{2} - \alpha } \right) + \cos \left( {\pi - \alpha } \right) + \cos \left( {\dfrac{{3\pi }}{2} - \alpha } \right) + \cos \left( {2\pi - \alpha } \right)\); f) \(\sin \left( {\dfrac{{5\pi }}{2} - \alpha } \right) - \cos \left( {\dfrac{{13\pi }}{2} - \alpha } \right) - 3\sin \left( {\alpha - 5\pi } \right) - 2\sin \alpha - \cos \alpha ;\) g) \(\cos \left( {5\pi + \alpha } \right) - 2\sin \left( {\dfrac{{11\pi }}{2} - \alpha } \right) - \sin \left( {\dfrac{{11\pi }}{2} + \alpha } \right)\). Giải: a) 0; b) 0; c) \(2\sin \alpha \); d) \( - 2\sin \alpha ;\) e) 0; f) 0 g) \(2\cos \alpha \) Sachbaitap.com
Xem thêm tại đây:
Bài 3. Giá trị lượng giác của các góc (cung) có liên quan đặc biệt
|

 Tải ngay
Tải ngay