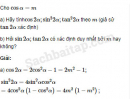Câu 6.45 trang 204 SBT Đại số 10 Nâng caoGiải bài tập Câu 6.45 trang 204 SBT Đại số 10 Nâng cao a) Cho \(\cos \alpha = 0,6\) và \(0 < \alpha < \dfrac{\pi }{2}\). Hãy tính \(\cos \dfrac{\alpha }{2};\sin \dfrac{\alpha }{2};\tan \dfrac{\alpha }{2}.\) b) Cho \(\sin \beta = \dfrac{3}{5}\) và \(\dfrac{\pi }{2} < \beta < \pi \). Hãy tính \(\cos \dfrac{\beta }{2};\sin \dfrac{\beta }{2};\tan \dfrac{\beta }{2}\). Giải: a) \(\begin{array}{l}\cos \dfrac{\alpha }{2} = \sqrt {\dfrac{{1 + \cos \alpha }}{2}} = \dfrac{{2\sqrt 5 }}{5};\\\sin \dfrac{\alpha }{2} = \sqrt {\dfrac{{1 - \cos \alpha }}{2}} = \dfrac{{\sqrt 5 }}{5};\\\tan \dfrac{\alpha }{2} = \dfrac{1}{2}.\end{array}\) b) \(\begin{array}{l}\cos \beta = - \sqrt {1 - \dfrac{9}{{25}}} = - \dfrac{4}{5};\\\cos \dfrac{\beta }{2} = \sqrt {\dfrac{{1 - \dfrac{4}{5}}}{2} = } = \dfrac{1}{{\sqrt {10} }};\\\sin \dfrac{\beta }{2} = \sqrt {\dfrac{{1 + \dfrac{4}{5}}}{2}} = \dfrac{3}{{\sqrt {10} }};\tan \dfrac{\beta }{2} = 3.\end{array}\) Sachbaitap.com
Xem thêm tại đây:
Bài 4. Một số công thức lượng giác
|

 Tải ngay
Tải ngay