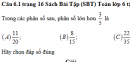Câu 6.5, 6.6, 6.7, 6.8 trang 16,17 Sách Bài Tập (SBT) Toán lớp 6 tập 2

Câu 6.5 trang 16 Sách Bài Tập (SBT) Toán lớp 6 tập 2

a) Cho phân số \({a \over b}\) (a, b ∈ N, b # 0)

 Giả sử  \({a \over b} > 1\) và m ∈ N, m # 0. Chứng tỏ rằng:

\({a \over b} < {{a + m} \over {b + m}}\)  

b) Áp dụng kết quả ở câu a) để so sánh \({{434} \over {561}}\) và \({{441} \over {568}}\) 

Giải

a) \({a \over b} = {{a(b + m)} \over {b(b + m)}} = {{ab + am} \over {{b^2} + bm}}\)                           (1)

\({{a + m} \over {b + m}} = {{b(a + m)} \over {b(b + m)}} = {{ab + bm} \over {{b^2} + bm}}\)               (2)

\({a \over b} < 1\) => a < b suy ra ab + am < ab + bm          (3)

Từ (1), (2) và (3) ta có: \({a \over b} < {{a + m} \over {b + m}}\) 

b) Áp dụng: Rõ ràng \({{434} \over {561}} < 1\) nên \({{434} \over {561}} < {{434 + 7} \over {561 + 7}} = {{441} \over {568}}\) 

Câu 6.6 trang 17 Sách Bài Tập (SBT) Toán lớp 6 tập 2

a) Cho phân số \({a \over b}\)  (a, b ∈ N, b # 0)

Giả sử \({a \over b} > 1\) và m ∈ N, m # 0. Chứng tỏ rằng

\({a \over b} > {{a + m} \over {b + m}}\)    

b) Áp dụng kết quả ở câu a) để so sánh \({{237} \over {142}}\) và \({{237} \over {142}}\) 

Giải

a) Giải tương tự bài 6.5 a)

b)  \({{237} \over {142}} > 1\) nên \({{237} \over {142}} < {{237 + 9} \over {142 + 9}} = {{246} \over {151}}\) 

Câu 6.7 trang 17 Sách Bài Tập (SBT) Toán lớp 6 tập 2

So sánh: \(A = {{{{17}^{18}} + 1} \over {{{17}^{19}} + 1}}\) và \(B = {{{{17}^{17}} + 1} \over {{{17}^{18}} + 1}}\)

Giải

\(A = {{{{17}^{18}} + 1} \over {{{17}^{19}} + 1}} < 1 \Rightarrow A = {{{{17}^{18}} + 1} \over {{{17}^{19}} + 1}} < {{{{17}^{18}} + 1 + 16} \over {{{17}^{19}} + 1 + 16}} = {{{{17}^{18}} + 17} \over {{{17}^{19}} + 17}}\) 

\({{17.({{17}^{17}} + 1)} \over {17.({{17}^{18}} + 1)}} = {{{{17}^{17}} + 1} \over {{{17}^{18}} + 1}} = B\)                 

Vậy A < B

Câu 6.8 trang 17 Sách Bài Tập (SBT) Toán lớp 6 tập 2

So sánh: \(C = {{{{98}^{99}} + 1} \over {{{98}^{89}} + 1}}\) và \(D = {{{{98}^{98}} + 1} \over {{{98}^{88}} + 1}}\) 

Giải

\(C = {{{{98}^{99}} + 1} \over {{{98}^{89}} + 1}} > 1 \Rightarrow C = {{{{98}^{99}} + 1} \over {{{98}^{89}} + 1}} > {{{{98}^{99}} + 1 + 97} \over {{{98}^{89}} + 1 + 97}} = {{{{98}^{99}} + 198} \over {{{98}^{89}} + 98}}\) 

\({{98.({{98}^{98}} + 1)} \over {98.({{98}^{88}} + 1)}} = {{{{98}^{98}} + 1} \over {{{98}^{88}} + 1}} = D\)                                 

 Sachbaitap.com