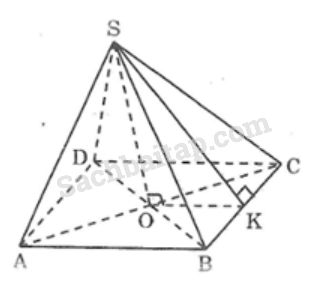
Câu 65 trang 151 Sách bài tập (SBT) Toán 8 tập 21. Kim tự tháp Kê-ốp (Thế kỉ 25 trước Công nguyên) là một hình chóp tứ giác đều, cạnh đáy bằng 233m, chiều cao hình chóp 146,5m. 1. Kim tự tháp Kê-ốp (Thế kỉ 25 trước Công nguyên) là một hình chóp tứ giác đều, cạnh đáy bằng 233m, chiều cao hình chóp 146,5m. a. Độ dài cạnh bên là bao nhiêu ? b. Tính diện tích xung quanh của hình chóp. c. Tính thể tích hình chóp. 2. Kim tự tháp Lu-vrơ (Louvre) (Xây dựng vào năm 1988). Người ta làm mô hình một kim tự tháp ở cổng vào của bảo tàng Lu-vrơ (Pháp). Mô hình có dạng chóp đều chiều cao 21m, độ dài cạnh đáy là 34m. a. Cạnh bên của hình chóp là bao nhiêu ? b. Tính thể tích hình chóp. c. Tính tổng diện tích các tấm kính để phủ lên hình chóp này (Sxq). Giải:
Giả sử các kim tự tháp là hình chóp tứ giác đều S.ABCD. a. Áp dụng định lí Pi-ta-go vào tam giác vuông AOB, ta có: \(O{A^2} + O{B^2} = A{B^2}\) Suy ra: \(2.O{A^2} = A{B^2}\) Suy ra: \(O{A^2} = {{A{B^2}} \over 2} = 27144,5\) Áp dụng định lí Pi-ta-go vào tam giác vuông SOA, ta có: \(\eqalign{ & S{A^2} = S{O^2} + O{A^2} \cr & = 146,{5^2} + 27144,{5} = 48606,75 \cr & SA = \sqrt {48606,75} \approx 220,5(cm) \cr} \) b. Kẻ SK ⊥ BC. Ta có: \(BK = KC = {1 \over 2}BC = 116,5(m)\) Áp dụng định lí Pi-ta-go vào tam giác vuông SIB, ta có: \(S{B^2} = S{K^2} + B{K^2}\) Suy ra: \(\eqalign{ & S{K^2} = S{B^2} - B{K^2} \cr & = 48606,75 - 13572,25 = 35034,5 \cr & SK = \sqrt {35034,5} \cr} \) Diện tích xung quanh của kim tự tháp là: \(S = \left( {233.2} \right).\sqrt {35034,5} \approx 87223,6({m^2})\) c) Thể tích hình chóp là: \(V = {1 \over 3}S.h = {1 \over 3}.233.233.146,5 = 2651112,8({m^3})\) 2. Tương tự câu 1. a) \(\sqrt {1019} \approx 31,9\;m\) b) \(8092\,{m^3}\) c) \(68\sqrt {730} \approx 1837,3\,{m^2}\) Sachbaitap.com
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 9. Thể tích của hình chóp đều
|
-
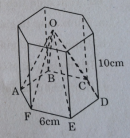
Câu 66 trang 152 Sách bài tập (SBT) Toán 8 tập 2
Thể tích hình chóp đều cho theo các kích thước ở hình 150 là:
-
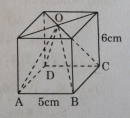
Câu 67 trang 152 Sách bài tập (SBT) Toán 8 tập 2
Tính thể tích hình chóp tứ giác đều O.ABCD (các kích thước cho trên hình 151)
-
Câu 68 trang 152 Sách bài tập (SBT) Toán 8 tập 2
Hình chóp tứ giác đều có độ dài cạnh bên là 5cm, chiều cao hình chóp là 4cm. Thể tích của hình chóp là:
-
Câu 69 trang 152 Sách bài tập (SBT) Toán 8 tập 2
Tính diện tích toàn phần của hình chóp đều sau đây:

 Tải ngay
Tải ngay