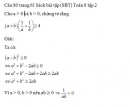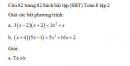Câu 78 trang 61 Sách bài tập (SBT) Toán 8 tập 2

Bình chọn:

3.3 trên 3 phiếu

Chứng tỏ rằng, trong một tam giác thì độ dài một cạnh luôn nhỏ hơn nửa chu vi.

Giải:

Gọi a, b, c lần lượt là độ dài ba cạnh của tam giác.

Chu vi tam giác là a + b + c.

Theo bất đẳng thức tam giác, ta có:

\(a < b + c \Leftrightarrow a + a < a + b + c\)

\(\Leftrightarrow 2a < a + b + c \Leftrightarrow a < {{a + b + c} \over 2}\)

Tương tự:

\(\eqalign{ & b < a + c \Leftrightarrow b + b < a + b + c \cr&\Leftrightarrow 2b < a + b + c \Leftrightarrow b < {{a + b + c} \over 2} \cr & c < a + b \Leftrightarrow c + c < a + b + c \cr&\Leftrightarrow 2c < a + b + c \Leftrightarrow c < {{a + b + c} \over 2} \cr} \)

Vậy trong một tam giác độ dài một cạnh luôn nhỏ hơn nửa chu vi.

Sachbaitap.com

Báo lỗi - Góp ý

Xem lời giải SGK - Toán 8 - Xem ngay

>> Học trực tuyến lớp 8 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.