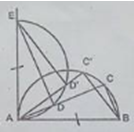
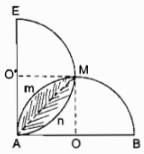
Câu 79 trang 114 Sách Bài Tập (SBT) Toán 9 Tập 2

Cho nửa đường tròn đường kính AB. Gọi C là một điểm chạy trên nửa đường tròn đó. Trên AC lấy điểm D sao cho AD = CD. Qua A kẻ tiếp tuyến với nửa đường tròn rồi lấy AE = AB (E và C cùng thuộc một nửa mặt phẳng bờ AB)

a) Tìm quỹ tích điểm D

b) Tính diện tích phần chung của hai nửa hình tròn đường kính AB và AE.

Giải

a) Chứng minh thuận

Nối DE. Xét ∆ABC và ∆AED:

AB = AE (gt)

AD = BC (gt)

\(\widehat {EAD} = \widehat {ABC}\) (hệ quả góc giữa tia tiếp tuyến và dây cung)

Suy ra: ∆ABC = ∆EAD (c.g.c) \( \Rightarrow \widehat {EAD} = \widehat {ACB}\)

Mà \(\widehat {ACB} = {90^0}\) (góc nội tiếp chắn nửa đường tròn)

\( \Rightarrow \widehat {EDA} = {90^0}\)

Điểm C chuyển động trên nửa đường tròn đường kính AB thì điểm D luôn nhìn đoạn AE cố định dưới một góc bằng 90⁰, nên điểm D nằm trên nửa đường tròn đường kính AE nằm trong nửa mặt phẳng bờ AE chứa nửa đường tròn đường kính AB.

Chứng minh đảo:

Trên nửa đường tròn đường kính AE lấy điểm D’ bất kỳ, đường thẳng AD’ cắt nửa đường tròn đường kính AB tại C’. Nối ED’, BC’.

Xét ∆AD'E và ∆BC'A:

\(\widehat {D'} = \widehat {C'} = {90^0}\) (các góc nội tiếp chắn nửa đường tròn)

AE = AB (gt)

\(\widehat {EAD} = \widehat {ABC'}\) (2 góc cùng phụ \(\widehat {C'AB}\))

Suy ra: ∆AD'E = ∆BC'A (cạnh huyền, góc nhọn)

                        \( \Rightarrow AD' = BC'\)

Vậy khi điểm C chạy trên nửa đường tròn đường kính AB thì quỹ tích điểm D là nửa đường tròn đường kính AE.

b) Gọi tâm hai nửa đường tròn đường kính AB và AE lần lượt là O và O’, giao điểm thứ hai của hai đường tròn là M

Ta có: OA = OM = O’A = O’M (vì AB = AE)

\(\widehat A = {90^0}\)

Vậy tứ giác AOMO’ là hình vuông

Diện tích phần chung của hai nửa hình tròn bằng diện tích hai quạt tròn có cung \(\overparen{AmM}\) trừ đi diện tích hình vuông

Diện tích hình quạt tròn AOM bằng:

\({{\pi {{\left( {{{AB} \over 2}} \right)}^2}.90} \over {360}} = {{\pi A{B^2}} \over {16}}\)

Diện tích của hình vuông AOMO’ bằng:

\({\left( {{{AB} \over 2}} \right)^2} = {{A{B^2}} \over 4}\)

Diện tích phần chung bằng:

\(2.{{\pi A{B^2}} \over {16}} - {{A{B^2}} \over 4} = {{\pi A{B^2}} \over 8} - {{2A{B^2}} \over 8}\)

                        \( = {{A{B^2}} \over 8}\left( {\pi  - 2} \right)\)  (đơn vị diện tích)

Sachbaitap.com