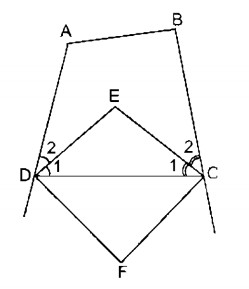
Câu 8 trang 80 Sách bài tập (SBT) Toán 8 tập 1Các tia phân giác của các góc C và D cắt nhau ở E. Các đường phân giác của các góc ngoài tại các đỉnh C và D cắt nhau ở F Tứ giác ABCD có \(\widehat A = {110^0},\widehat B = {100^0}\). Các tia phân giác của các góc C và D cắt nhau ở E. Các đường phân giác của các góc ngoài tại các đỉnh C và D cắt nhau ở F. Tính \(\widehat {CED},\widehat {CFD}\) Giải:
- Trong tứ giác ABCD, ta có: \(\eqalign{ - Trong ∆CED, ta có: \(\widehat {CED} = {180^0} - \left( {{{\widehat C}_1} + {{\widehat D}_1}} \right) = {180^0} - {75^0} = {105^0}\) DE ⊥ DF (tính chất tia phân giác của hai góc kề bù) \(\Rightarrow \widehat {EDF} = {90^0}\) CE ⊥ CF (tính chất tia phân giác của hai góc kề bù) \( \Rightarrow \widehat {ECF} = {90^0}\) Trong tứ giác CEDF, ta có: \(\eqalign{ Sachbaitap.com
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 1. Tứ giác
|
-
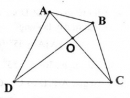
Câu 9 trang 80 Sách bài tập (SBT) Toán 8 tập 1
Chứng minh rằng trong một tứ giác, tổng hai đường chéo lớn hơn tổng hai cạnh đối.
-
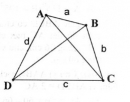
Câu 10 trang 80 Sách bài tập (SBT) Toán 8 tập 1
Chứng minh rằng trong một tứ giác, tổng hai đường chéo lớn hơn nửa chu vi nhưng nhỏ hơn chu vi của tứ giác ấy.

 Tải ngay
Tải ngay