Tải ngay
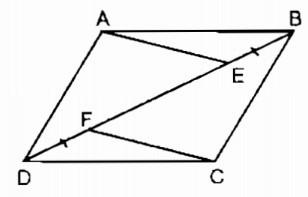
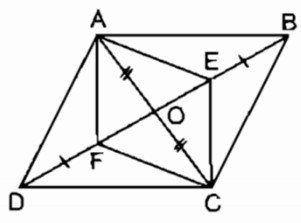
Câu 82 trang 90 Sách bài tập (SBT) Toán 8 tập 1Trên hình 10, cho ABCD là hình bình hành. Chứng minh rằng AE // CF. Trên hình 10, cho ABCD là hình bình hành. Chứng minh rằng AE // CF.
Giải:
Gọi O là giao điểm của AC và BD. OA = OC (tính chất hình bình hành) OB = OD (tính chất hình bình hành) BE = DF (gt) Ta có: OB = OE + BE OD = OF + DF Suy ra: OE = OF Do đó tứ giác AECF là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường) Suy ra AE // CF (tính chất hình bình hành). Sachbaitap.com
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.
Xem thêm tại đây:
Bài 7. Hình bình hành
|
-
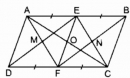
Câu 83 trang 90 Sách bài tập (SBT) Toán 8 tập 1
Chứng minh rằng : a. EMFN là hình bình hành. b. Các đường thẳng AC, EF, MN đồng quy.
-
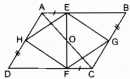
Câu 84 trang 90 Sách bài tập (SBT) Toán 8 tập 1
Trên hình 11, cho ABCD là hình bình hành. Chứng minh rằng:
-
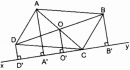
Câu 85 trang 90 Sách bài tập (SBT) Toán 8 tập 1
Cho hình bình hành ABCD. Qua C kẻ đường thẳng xy chỉ có một điểm chung C với hình bình hành. Gọi AA’, BB’, DD’ là các đường vuông góc kẻ từ A, B, D đến đường thẳng xy. Chứng ming rằng AA’ = BB’ + DD’.
-
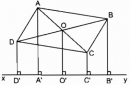
Câu 86 trang 90 Sách bài tập (SBT) Toán 8 tập 1
Cho hình bình hành ABCD và đường thẳng xy không có điểm chung với hình bình hành. Gọi AA’, BB’, CC’, DD’ là đường vuông góc kẻ từ A, B, C, D đến đường thẳng xy. Tìm mối liên hệ độ dài giữa AA’, BB’, CC’, DD’.
