Tải ngay
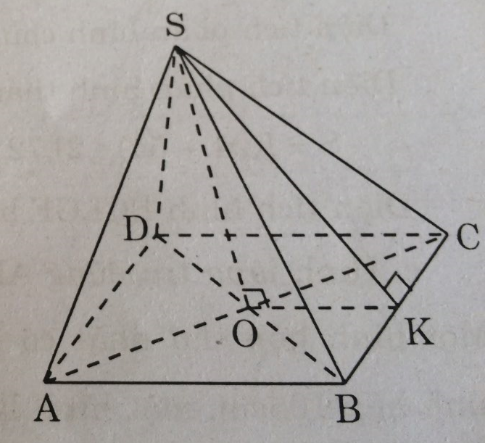
Câu 85 trang 156 Sách bài tập (SBT) Toán 8 tập 2Một hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy là 10cm, chiều cao hình chóp là 12cm. Tính: Một hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy là 10cm, chiều cao hình chóp là 12cm. Tính: a. Diện tích toàn phần của hình chóp b. Thể tích hình chóp. Giải: a. Gọi O là tâm của hình vuông đáy. Kẻ SK ⊥ BC, ta có: KB = KC = 5 cm Vì SO ⊥ (ABCD) nên SO ⊥ OK Trong tam giác SOK ta có: \(\widehat {SOK} = 90^\circ \) \(OK = {1 \over 2}AB = 5(cm)\) Áp dụng định lí Pi-ta-go vào tam giác vuông SOK, ta có: \(S{K^2} = S{O^2} + O{K^2} = {12^2} + {5^2} = 169\) Suy ra: SK = 13 (cm) Diện tích xung quanh hình chóp đều là: \(S = \left( {2.10} \right).13 = 260(c{m^2})\) Diện tích mặt đáy: \(S = 10.10 = 100(c{m^2})\) Diện tích toàn phần hình chóp đều là: \({S_{TP}} = 260 + 100 = 360(c{m^2})\) b. Thể tích hình chóp đều là: \(V = {1 \over 3}S.h = {1 \over 3}.100.12 = 400(c{m^3})\) Sachbaitap.com
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.
Xem thêm tại đây:
Ôn tập chương IV - Hình lăng trụ đứng. Hình chóp đều
|
-
Câu 87 trang 157 Sách bài tập (SBT) Toán 8 tập 2
Thể tích của một hình chóp đều là 126cm3, chiều cao của hình chóp là 6cm. Như vậy: Trong các số dưới đây, số nào là diện tích đáy của nó ?
-
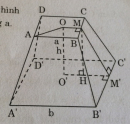
Câu 88 trang 157 Sách bài tập (SBT) Toán 8 tập 2
Cho hình chóp cụt tứ giác đều ABCD.A’B’C’D’ có các cạnh đáy là a và 2a, chiều cao của mặt bên là a.
-
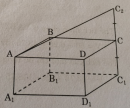
Câu 89 trang 157 Sách bài tập (SBT) Toán 8 tập 2
Cần phải đo đường chéo của một viên gạch có dạng hình hộp chữ nhật mà chỉ được phép sử dụng thước có chia vạch thì phải làm như thế nào ? (không được cắt, xẻ…)
