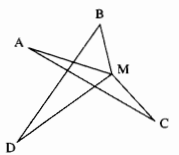
Câu 85 trang 53 Sách Bài Tập (SBT) Toán lớp 7 tập 2Hãy tìm một điểm M sao cho tổng MA + MB + MC + MD là nhỏ nhất. Cho bốn điểm A, B, C, D như hình dưới. Hãy tìm một điểm M sao cho tổng MA + MB + MC + MD là nhỏ nhất.
Giải Với M là điểm bất kỳ. Ta có M không trùng với giao điểm của AC và BD Trong ∆MBD ta có: MB + MD > BD (bất đẳng thức tam giác) Trong ∆MAC ta có: MA + MC > AC (bất đẳng thức tam giác) Nếu M trùng với giao điểm AC và BD \( \Rightarrow \) MA + MC = AC MB + MD = BD Vậy MA + MC ≥ AC MB + MD ≥ BD (dấu bằng xảy ra khi M trùng với giao điểm của AC và BD) \( \Rightarrow \) MA + MB + MC + MD ≥ AC + BD Vậy MA + MB + MC + MD = AC + BD bé nhất khi đó M là giao điểm của AC và BD Sachbaitap.com
Xem lời giải SGK - Toán 7 - Xem ngay >> Học trực tuyến lớp 7 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 7 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
|
-
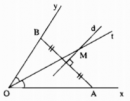
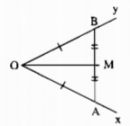
Câu 87 trang 53 Sách Bài Tập (SBT) Toán lớp 7 tập 2
a) Hãy tìm điểm M nằm trong góc xOy, cách đều Ox, Oy và cách đều A, B.
-
Câu 88 trang 53 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Dùng một chiếc thước thẳng có chia khoảng, hãy nêu cách vẽ tia phân giác của góc xOy.

 Tải ngay
Tải ngay